Windowing Functions

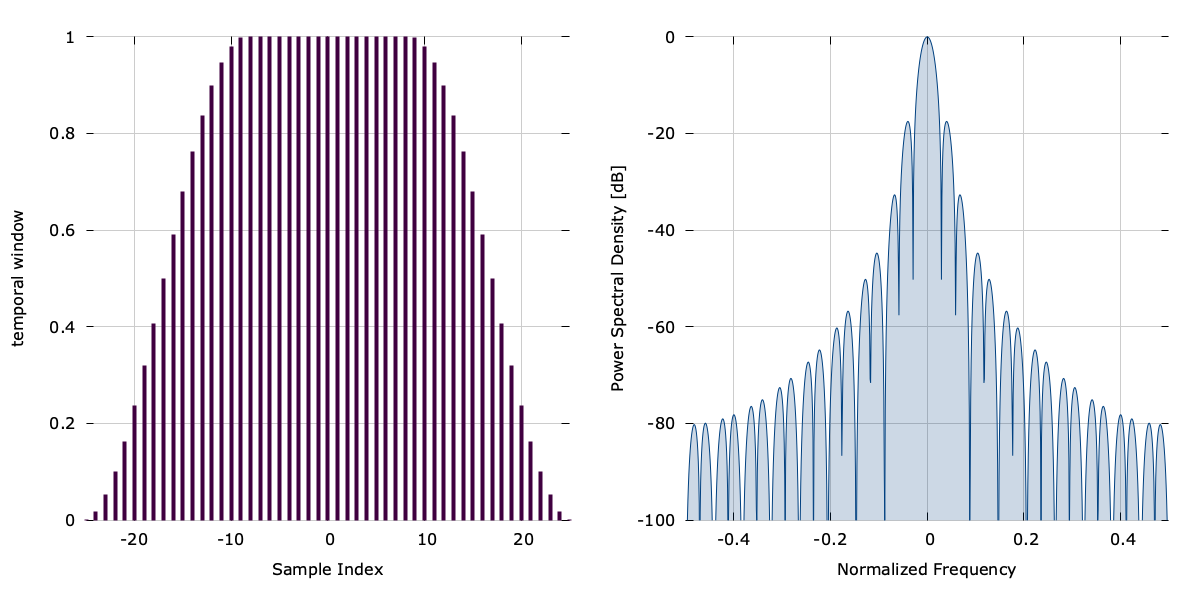
This section describes the various windowing functions in the math module. These windowing functions are useful for spectral approximation as they are compact in both the time and frequency domains.

hamming(), (Hamming window)∞

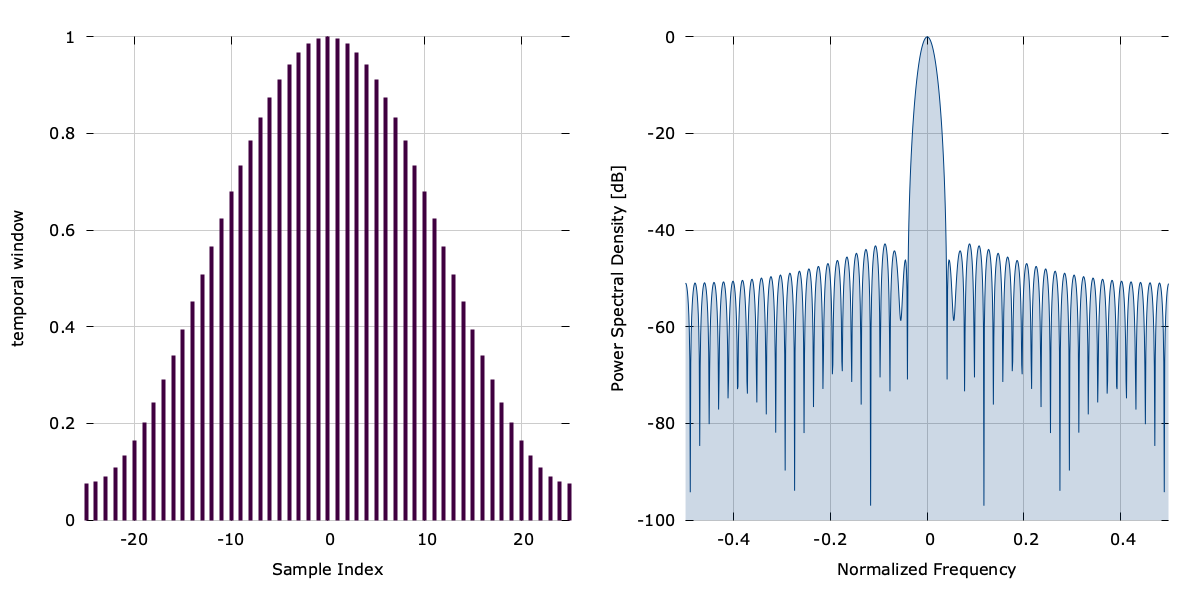
The function hamming(n,N) computes the $n^{th}$ of $N$ indices of the Hamming window:

$$ w(n) = 0.53836 - 0.46164 \cos\left( 2 \pi n / (N-1) \right) $$

hann(), (Hann window)∞

The function hann(n,N) computes the $n^{th}$ of $N$ indices of the Hann window:

$$ w(n) = 0.5 - 0.5 \cos\left( 2 \pi n / (N-1) \right) $$

blackmanharris(), (Blackman-harris window)∞

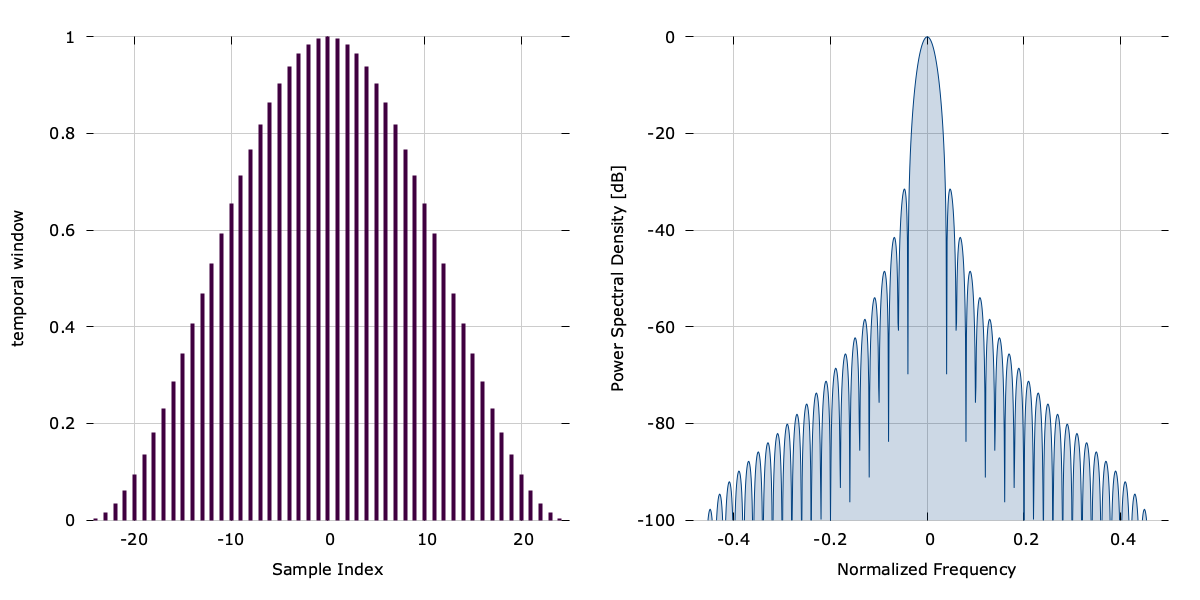
The function blackmanharris(n,N) computes the $n^{th}$ of $N$ indices of the Blackman-harris window:

$$ w(n) = \sum_{k=0}^{3} { a_k \cos\left( 2 \pi k n / (N-1)\right) } $$

where$a_0 = 0.35875$ ,$a_1 = -0.48829$ ,$a_2 = 0.14128$ , and$a_3 = -0.01168$ .

blackmanharris7(), (7th-order Blackman-harris window)∞

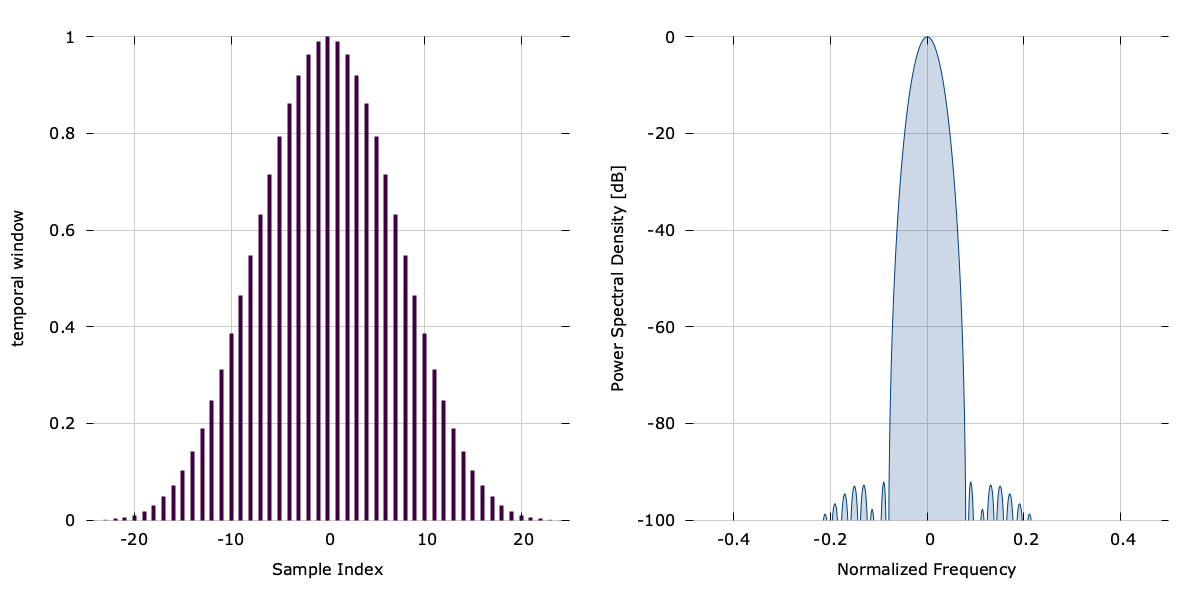
The function blackmanharris7(n,N) computes the $n^{th}$ of $N$ indices of the 7$^{th}$ -order Blackman-harris window:

$$ w(n) = \sum_{k=0}^{3} { a_k \cos\left( 2 \pi k n / (N-1)\right) } $$

where$a_0 = 0.27105$ ,$a_1 = 0.43329$ ,$a_2 = 0.21812$ ,$a_3 = 0.06592$ ,$a_4 = 0.01081$ ,$a_5 = 0.00077$ , and$a_6 = 0.00001$ .

Notice that the side-lobes have been suppressed below 100 dB at the expense of a wider main lobe.

doc/windowing/window_blackmanharris7.png

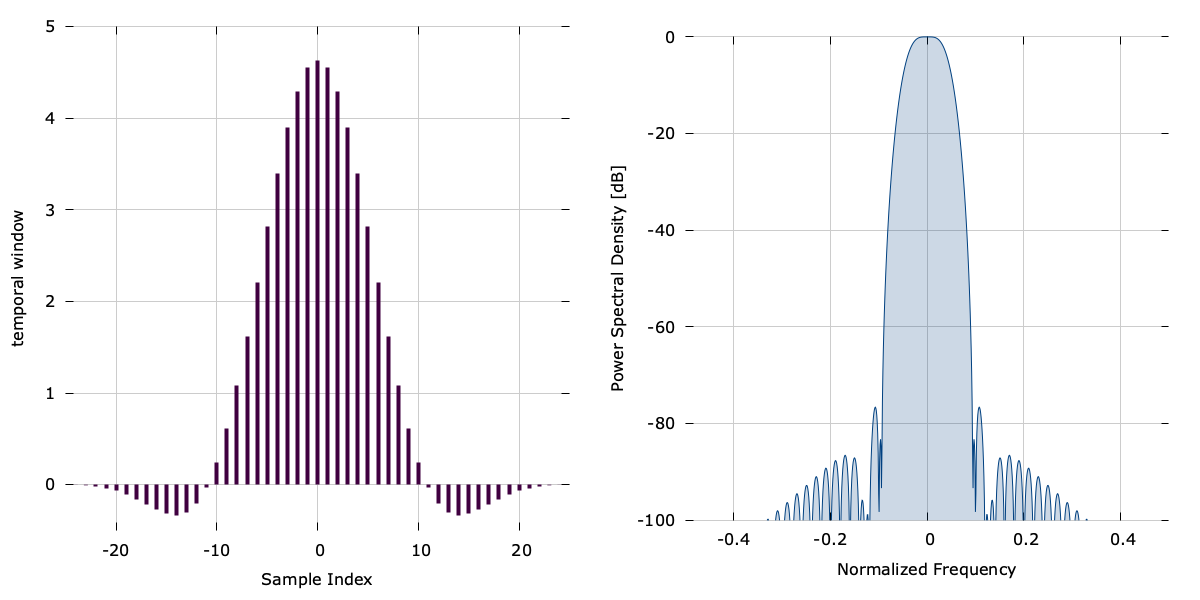
flattop(), (Flat-top window)∞

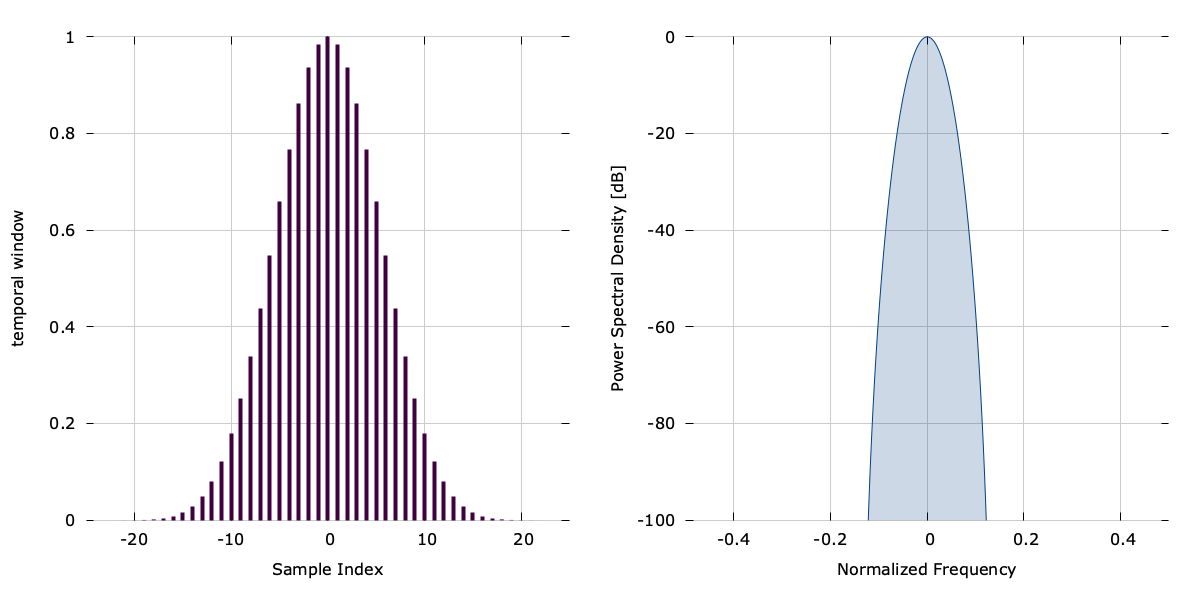
The function flattop(n,N) computes the $n^{th}$ of $N$ indices of the Flat-top window:

$$ w(n;N) = 1 - 1.93 \cos\left( \frac{n}{N}\right) + 1.29 \cos\left(2\frac{n}{N}\right) - 0.388\cos\left(3\frac{n}{N}\right) + 0.028\cos\left(4\frac{n}{N}\right) $$

Notice that the response looks similar to a low-pass non-recursive [ref:filter design][ref:/doc/firdes/] , allows the window to have negative values, and has a peak much greater than one.

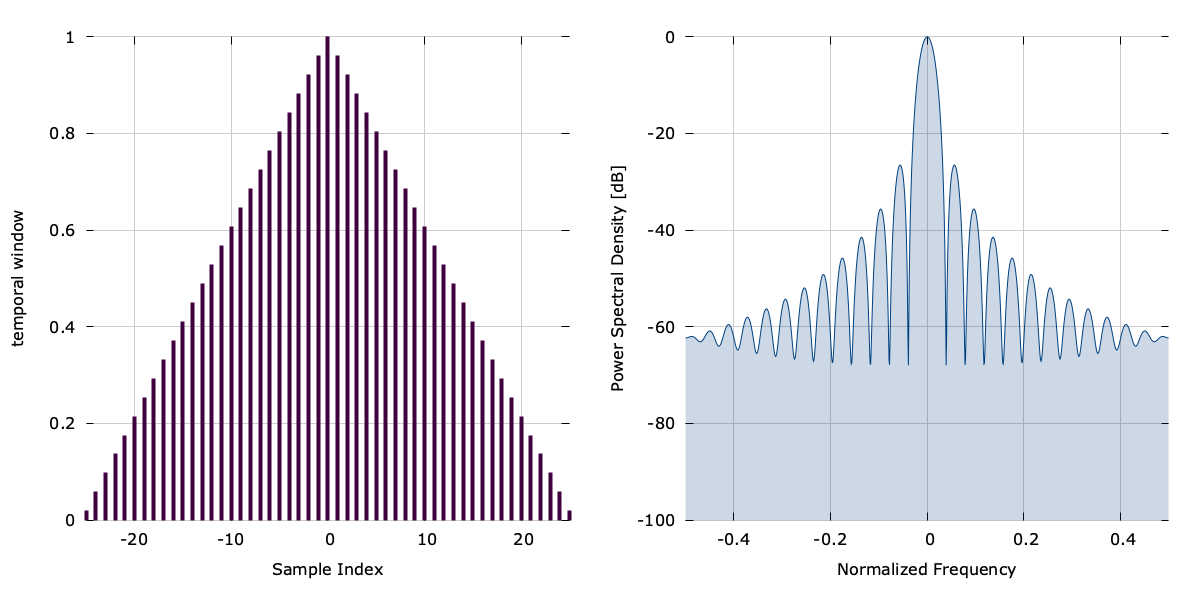
triangular(), (Triangular window)∞

The function triangular(n,N,L) computes the $n^{th}$ of $N$ indices of the triangular window:

$$ w(n;N) = 1 - \left| \frac{n - \frac{N-1}{2} }{\frac{L}{2}}\right| $$

kaiser(), (Kaiser-Bessel window)∞

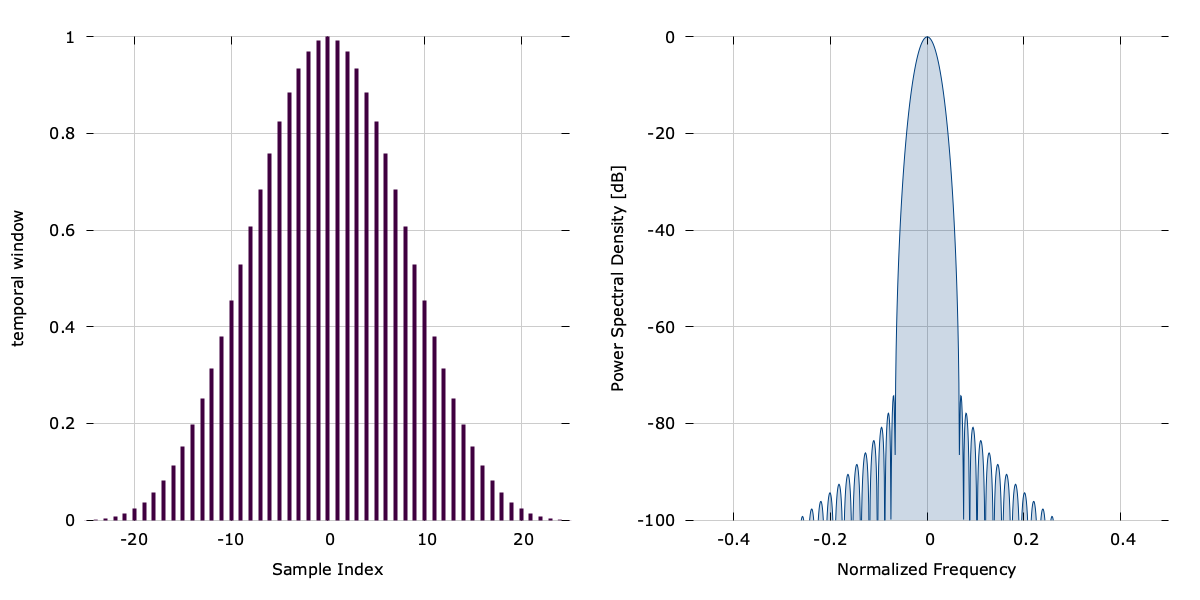
The function kaiser(n,N,beta) computes the $n^{th}$ of $N$ indices of the Kaiser-$\beta$ window with a shape parameter $\beta$ :

$$ w(n,\beta) = \frac{ I_0\left(\pi\beta\sqrt{1-\left(\frac{n}{N/2}\right)^2}\right) }{ I_0\left(\pi\beta\right) } $$

where $I_\nu(z)$ is the modified Bessel function of the first kind of order $\nu$ , and $\beta$ is a parameter controlling the width of the window and its stop-band attenuation. In liquid , $I_0(z)$ is computed using liquid_besseli0f() (see [ref:section-math-transcendentals] ). A fractional sample offset $\Delta t$ can be introduced by substituting$\frac{n}{N/2}$ with$\frac{n+\Delta t}{N/2}$ in [ref:eqn-math-window-kaiser] .

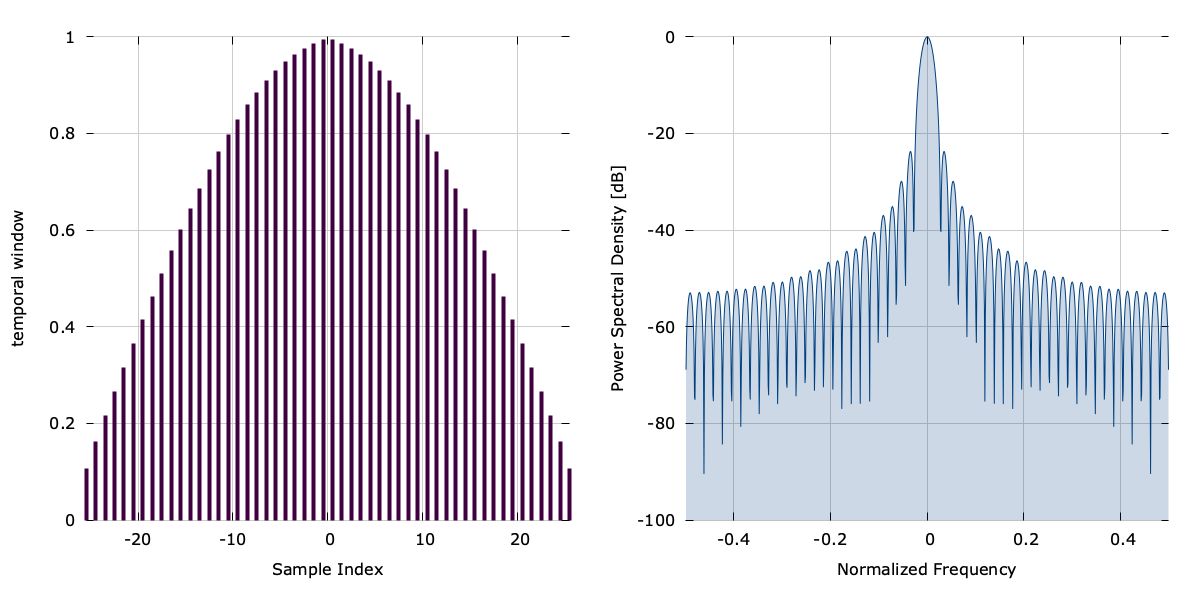
liquid_kbd_window(), (Kaiser-Bessel derived window)∞

The function liquid_kbd_window(n,beta,*w) computes the $n$ -point Kaiser-Bessel derived window with a shape parameter $\beta$ storing the result in the $n$ -point array w . The length of the window must be even.

liquid_rcostaper_windowf(), (raised-cosine tapering window)∞

The function liquid_rcostaper_windowf(n,t,N) computes the $n^{th}$ of $N$ indices of the raised-cosine tapering window with t samples on the front and tail used for tapering.