Spectral Periodogram (spgram)

In harmonic analysis, the spectral periodogram is an estimate of the spectral density of a signal over time. For a signal \(x(t)\) , the spectral content at time \(t_0\) may be estimated over a time duration of \(T\) seconds as

$$ \hat{X}_{t_0}(\omega) = \frac{1}{T} \int_{0}^{T} { x(t-t_0)w(t)e^{-j\omega t} dt } $$

where \(w(t) = 0,\forall t \notin (0,T)\) is a temporal windowing function to smooth transitions between transforms. Typical windowing functions are the Hamming, Hann, and Kaiser windows (see window methods for a description and spectral representation of available windowing functions in liquid ). Internally, the spgram object using the Hamming window.

.. footnote:
Future development may permit the user to specify which
windowing method is preferred.

For a discretely-sampled signal \(x(nT_s)\) , the spectral content at time index \(p\) is

$$ \hat{X}_p(k) = \frac{1}{N} \sum_{i=0}^{N-1}{ x((i+p)T_s) w(iT_s) e^{-j 2 \pi k i/N} } $$

which is simply the \(N\) -point discrete Fourier transform of the input sequence indexed at \(p\) with a shaping window applied.

[ref:fig-spgram-diagram] depicts a spectral periodogram for the discrete case in which two overlapping transforms are taken with a delay between them. The windowing function provides time localization at the expense of frequency resolution. Typically the length of the window is half the size of the transform, and the delay is a quarter the size of the transform.

liquid implements a discrete spectral periodogram with the spgram object. Listed below is the full interface to the spgram object.

• spgram_create(nfft,wtype,window_len,delay) creates and returns an spgram object with a transform size of nfft samples, a window type wtype , a window of window_len samples, and a delay between transforms of delay samples.
• spgram_create_default(nfft) creates and returns an spgram object with a transform size of nfft samples.
• spgram_destroy(q) destroys an spgram object, freeing all internally-allocated memory.
• spgram_reset(q) clears the internal spgram buffers.
• spgram_push(q,*x,n) pushes \(n\) samples of the array \(\vec{x}\) into the internal buffer of an spgram object.
• spgram_execute(q,*X) computes the spectral periodogram output storing the result in the nfft -point output array \(\vec{X}\) . The output array is of type float complex and contain output of the FFT.

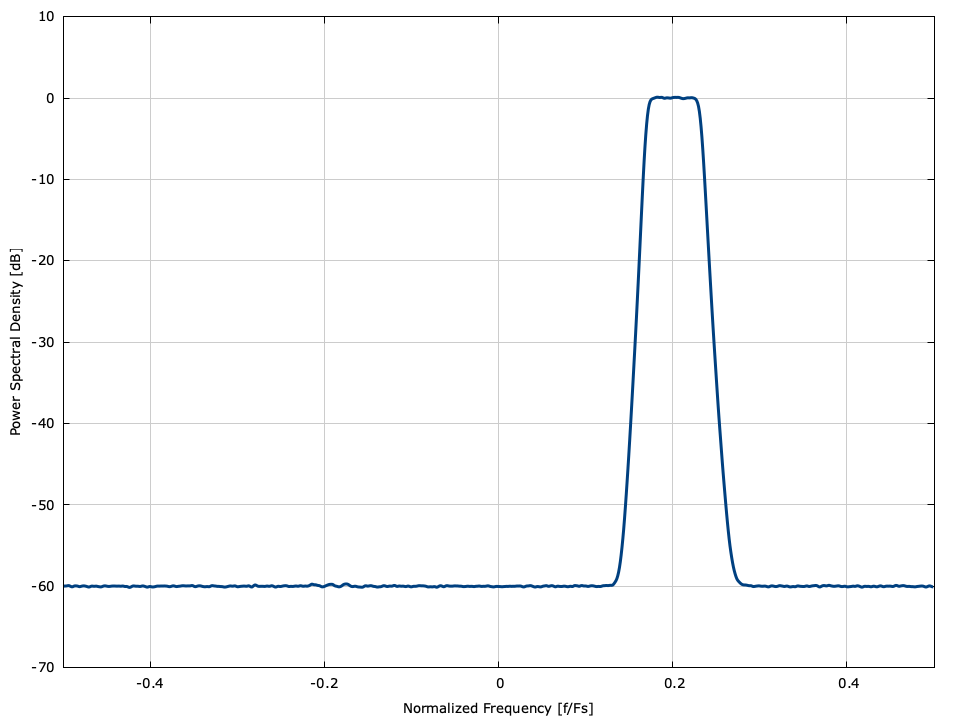
An example of the spgram object can be found in [ref:fig-spgram] in which band-limited signal is generated and analyzed.

#include <liquid/liquid.h>

int main() {
    // options
    unsigned int nfft    = 2401;    // FFT size
    unsigned int buf_len = 3456;    // input buffer size

    // create spectral periodogram
    spgramcf q = spgramcf_create_default(nfft);

    // allocated memory arrays
    float complex * buf = (float complex*) malloc(buf_len*sizeof(float complex));
    float         * psd = (float        *) malloc(nfft   *sizeof(float        ));

    // ... initialize input ...

    // write block of samples to spectral periodogram object
    spgramcf_write(q, buf, buf_len);

    // compute power spectral density output (repeat as necessary)
    spgramcf_get_psd(q, psd);

    // destroy object and free memory arrays
    spgramcf_destroy(q);
    free(buf);
    free(psd);
}