Maximal-length Sequence Generator (msequence)

The msequence object in liquid is really just a linear feedback shift register (LFSR), efficiently implemented using unsigned integers. The LFSR consists of an \(m\) -bit shift register, \(v\) , and generator polynomial\(g(x)\) . For primitive polynomials, the output sequence has a length \(n=2^m-1\) before repeating. This sequence is known as a maximal-length P/N (positive/negative) sequence, and consists of several useful properties:

the output sequence has very good auto-correlation properties; when aligned, the sequence, of course, correlates perfectly to \(n\) . When misaligned by any amount, however, the sequence correlates to exactly \(-1\) .
the sequence is easily generated using a linear feedback shift register

Only a certain subset of all possible generator polynomials produce this maximal length sequence.

Table [tab-sequence-genpoly]. Default \(m\) -sequence generator polynomials in liquid

\(m\)	\(n=2^m-1\)	\(g\) (hex)	liquid macro	\(g(x)\)
2	3	0x00000003	LIQUID_MSEQUENCE_GENPOLY_M2	\( x^{2} + x + 1 \)
3	7	0x00000006	LIQUID_MSEQUENCE_GENPOLY_M3	\( x^{3} + x^{2} + 1 \)
4	15	0x0000000c	LIQUID_MSEQUENCE_GENPOLY_M4	\( x^{4} + x^{3} + 1 \)
5	31	0x00000014	LIQUID_MSEQUENCE_GENPOLY_M5	\( x^{5} + x^{3} + 1 \)
6	63	0x00000030	LIQUID_MSEQUENCE_GENPOLY_M6	\( x^{6} + x^{5} + 1 \)
7	127	0x00000060	LIQUID_MSEQUENCE_GENPOLY_M7	\( x^{7} + x^{6} + 1 \)
8	255	0x000000b8	LIQUID_MSEQUENCE_GENPOLY_M8	\( x^{8} + x^{6} + x^{5} + x^{4} + 1 \)
9	511	0x00000110	LIQUID_MSEQUENCE_GENPOLY_M9	\( x^{9} + x^{5} + 1 \)
10	1,023	0x00000240	LIQUID_MSEQUENCE_GENPOLY_M10	\( x^{10} + x^{7} + 1 \)
11	2,047	0x00000500	LIQUID_MSEQUENCE_GENPOLY_M11	\( x^{11} + x^{9} + 1 \)
12	4,095	0x00000e08	LIQUID_MSEQUENCE_GENPOLY_M12	\( x^{12} + x^{11} + x^{10} + x^{4} + 1 \)
13	8,191	0x00001c80	LIQUID_MSEQUENCE_GENPOLY_M13	\( x^{13} + x^{12} + x^{11} + x^{8} + 1 \)
14	16,383	0x00003802	LIQUID_MSEQUENCE_GENPOLY_M14	\( x^{14} + x^{13} + x^{12} + x^{2} + 1 \)
15	32,767	0x00006000	LIQUID_MSEQUENCE_GENPOLY_M15	\( x^{15} + x^{14} + 1 \)
16	65,535	0x0000d008	LIQUID_MSEQUENCE_GENPOLY_M16	\( x^{16} + x^{15} + x^{13} + x^{4} + 1 \)
17	131,071	0x00012000	LIQUID_MSEQUENCE_GENPOLY_M17	\( x^{17} + x^{14} + 1 \)
18	262,143	0x00020400	LIQUID_MSEQUENCE_GENPOLY_M18	\( x^{18} + x^{11} + 1 \)
19	524,287	0x00072000	LIQUID_MSEQUENCE_GENPOLY_M19	\( x^{19} + x^{18} + x^{17} + x^{14} + 1 \)
20	1,048,575	0x00090000	LIQUID_MSEQUENCE_GENPOLY_M20	\( x^{20} + x^{17} + 1 \)
21	2,097,151	0x00140000	LIQUID_MSEQUENCE_GENPOLY_M21	\( x^{21} + x^{19} + 1 \)
22	4,194,303	0x00300000	LIQUID_MSEQUENCE_GENPOLY_M22	\( x^{22} + x^{21} + 1 \)
23	8,388,607	0x00420000	LIQUID_MSEQUENCE_GENPOLY_M23	\( x^{23} + x^{18} + 1 \)
24	16,777,215	0x00e10000	LIQUID_MSEQUENCE_GENPOLY_M24	\( x^{24} + x^{23} + x^{22} + x^{17} + 1 \)
25	33,554,431	0x01000004	LIQUID_MSEQUENCE_GENPOLY_M25	\( x^{25} + x^{3} + 1 \)
26	67,108,863	0x02000023	LIQUID_MSEQUENCE_GENPOLY_M26	\( x^{26} + x^{6} + x^{2} + x + 1 \)
27	134,217,727	0x04000013	LIQUID_MSEQUENCE_GENPOLY_M27	\( x^{27} + x^{5} + x^{2} + x + 1 \)
28	268,435,455	0x08000004	LIQUID_MSEQUENCE_GENPOLY_M28	\( x^{28} + x^{3} + 1 \)
29	536,870,911	0x10000002	LIQUID_MSEQUENCE_GENPOLY_M29	\( x^{29} + x^{2} + 1 \)
30	1,073,741,823	0x20000029	LIQUID_MSEQUENCE_GENPOLY_M30	\( x^{30} + x^{6} + x^{4} + x + 1 \)
31	2,147,483,647	0x40000004	LIQUID_MSEQUENCE_GENPOLY_M31	\( x^{31} + x^{3} + 1 \)

The default generator polynomials are listed in[ref:tab-sequence-genpoly] , however many more exist.

Notice that both the first and last coefficient of each generator polynomial\(g(x)\) is a \(1\) . This holds true for all \(m\) -sequence generator polynomials. The hexadecimal representation of the generator polynomial drops the trailing 1 as this value is implied in the shift register representation. A default generator polynomial for \(m=2\)\((n=3)\) through \(m=31\)\((n=2,147,483,647)\) are provided in the table, above. These default generator polynomials are included in the global liquid.h header file, as well, for convenience.

#include <liquid/liquid.h>

int main() {
    // create and initialize m-sequence (length 63)
    msequence q = msequence_create_default(6);

    // cycle through values and print state
    unsigned int i;
    for (i=0; i<msequence_get_length(q); i++) {
        printf("%u\n",msequence_get_state(q));
        msequence_advance(q);
    }

    // destroy object
    msequence_destroy(q);
}

Shown above is a short example program demonstrating how to create an msequence object using the default generator polynomial. The program cycles through the entire sequence and prints the internal state of the shift register, a unique sequence for all values in \(1 \ldots n-1\) , but in a pseudo-random order.

Figure [fig-sequence-msequence]. msequence auto-correlation, \(m=7\) (\(n=127\) ), \(g=\) 0x60

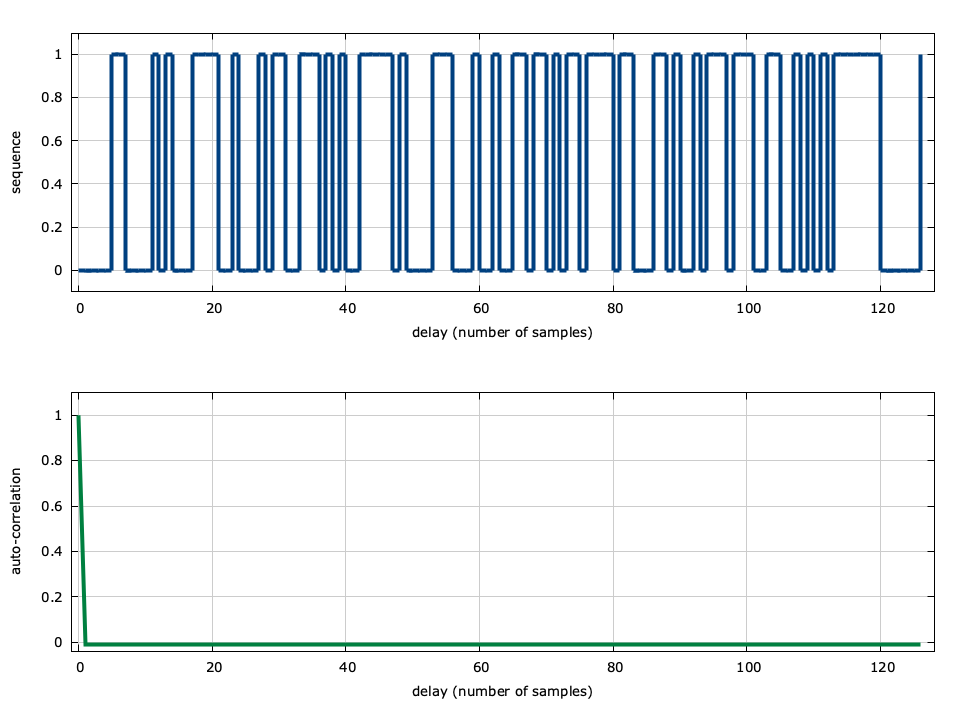
The auto-correlation of the \(m\) -sequence with generator polynomial\(g=\) 0x60 can be seen in [ref:fig-sequence-msequence] . The shift register has seven bits (\(m=7\) ) and therefore the output sequence is of length \(n=2^m-1=127\) . Notice that the auto-correlation is equal to unity with no delay, and nearly zero (\(-1/127\) ) for all other delays.

Maximal-length Sequence Generator (msequence)

Overview

Documents

Source Code