Infinite Impulse Response Filter (iirfilt)

The iirfilt_crcf object and family implement the infinite impulse response (IIR) filters. Also known as recursive filters, IIR filters allow a portion of the output to be fed back into the input, thus creating an impulse response which is non-zero for an infinite amount of time. Formally, the output signal \(y[n]\) may be written in terms of the input signal\(x[n]\) as

$$ y[n] = \frac{1}{a_0} \left( \sum_{j=0}^{n_b-1}{ b_j x[n-j] } - \sum_{k=1}^{n_a-1}{ a_k y[n-k] } \right) $$

where \(\vec{b} = [b_0,b_1,\ldots,b_{n_b-1}]^T\) are the feed-forward parameters and \(\vec{a} = [a_0,a_1,\ldots,a_{n_a-1}]^T\) are the feed-back parameters of length \(n_b\) and \(n_a\) , respectively. The \(z\) -transform of the transfer function is therefore

$$ H(z) = \frac{Y(z)}{X(z)} = \frac{\sum\limits_{j=0}^{n_b-1}{b_j z^{-j}}} {\sum\limits_{k=0}^{n_a-1}{a_k z^{-k}}} = \frac{ b_0 + b_1 z^{-1} + \cdots + b_{n_b-1} z^{n_b-1}} { a_0 + a_1 z^{-1} + \cdots + a_{n_a-1} z^{n_a-1}} $$

Typically the coefficients in \(H(z)\) are normalized such that \(a_0=1\) .

For larger order filters (even as small as \(n\approx 8\) ) the filter can become unstable due to finite machine precision. It is often therefore useful to express \(H(z)\) in terms of second-order sections. For a filter of order \(n\) , these sections are denoted by the two\((L+r)\times 3\) matrices \(\vec{B}\) and \(\vec{A}\) where \(r=n \mod 2\) (0 for odd \(n\) , 1 for even \(n\) ) and \(L=(n-r)/2\) .

$$ H_d(z) = \left[ \frac{B_{r,0} + B_{r,1}z^{-1}} {1 + A_{r,1}z^{-1}} \right]^r \prod_{k=1}^{L} {\left[ \frac{B_{k,0} + B_{k,1}z^{-1} + B_{k,2}z^{-2}} {1 + A_{k,1}z^{-1} + A_{k,2}z^{-2}} \right]} $$

Notice that \(H(z)\) is now a series of cascaded second-order IIR filters. The sos form is practical when filters are designed from analog prototypes where the poles and zeros are known. liquid implements second-order sections efficiently with the internal iirfiltsos_crcf family of objects. For a cascaded second-order section IIR filter, use iirfilt_crcf_create_sos(B,A,n) . See also : iirdes (IIR filter design) in[ref:section-filter-iirdes] .

Listed below is the full interface to the iirfilt family of objects. The interface to the iirfilt object follows the convention of other liquid signal processing objects; while each method is listed for iirfilt_crcf , the same functionality applies to iirfilt_rrrf and iirfilt_cccf .

• iirfilt_crcf_create(*b,Nb,*a,Nb) creates a new iirfilt object with\(N_b\) feed-forward coefficients \(\vec{b}\) and\(N_a\) feed-back coefficients \(\vec{a}\) .
• iirfilt_crcf_create_sos(*B,*A,Nsos) creates a new iirfilt object using \(N_{sos}\) second-order sections. The \([N_{sos} \times 3]\) feed-forward coefficient matrix is specified by \(\vec{B}\) and the \([N_{sos} \times 3]\) feed-back coefficient matrix is specified by \(\vec{A}\) .
• iirfilt_crcf_create_prototype(ftype,btype,format,order,fc,f0,Ap,As) creates a new IIR filter object using the prototype interface described in [ref:section-filter-iirdes-iirdes] . This is the simplest method for designing an IIR filter with Butterworth, Chebyshev-I, Chebyshev-II, elliptic/Cauer, or Bessel coefficients.
• iirfilt_crcf_destroy(q) destroys an iirfilt object, freeing all internally-allocated memory arrays and buffers.
• iirfilt_crcf_print(q) prints the internals of an iirfilt object.
• iirfilt_crcf_clear(q) clears the filter's internal state.
• iirfilt_crcf_execute(q,x,*y) executes one iteration of the filter with an input \(x\) , storing the result in \(y\) , and updating its internal state.
• iirfilt_crcf_get_length(q) returns the order of the filter.
• iirfilt_crcf_freqresponse(q,fc,*H) computes the complex response \(H\) of the filter at the normalized frequency \(f_c\) .
• iirfilt_crcf_groupdelay(q,fc) returns the group delay of the filter at the normalized frequency \(f_c\) .

Listed below is a basic example of the interface. For more detailed and extensive examples, refer to examples/iirfilt_crcf_example.c in the main liquid project source directory.

#include <liquid/liquid.h>

int main() {
    // options
    unsigned int order=4;   // filter order

    unsigned int n = order+1;
    float b[n], a[n];

    // ... initialize filter coefficients ...

    // create filter object
    iirfilt_crcf q = iirfilt_crcf_create(b,n,a,n);

    float complex x;    // input sample
    float complex y;    // output sample

    // execute filter (repeat as necessary)
    iirfilt_crcf_execute(q,x,&y);

    // destroy filter object
    iirfilt_crcf_destroy(q);
}

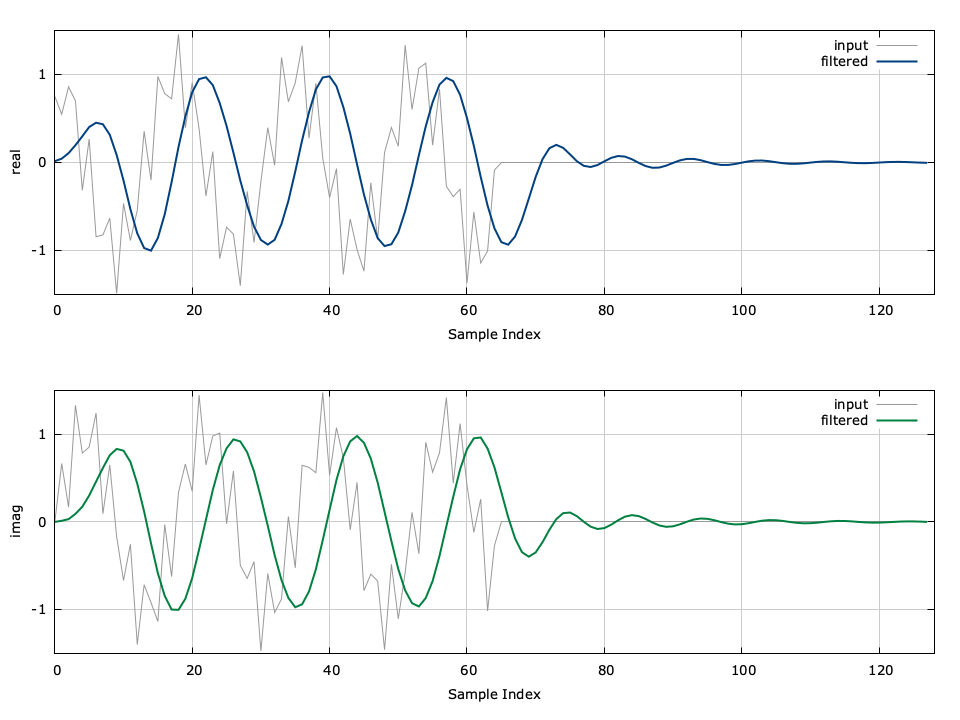
An example of the iirfilt can be seen in[ref:fig-filter-iirfilt_crcf] in which a low-pass filter is applied to a signal to remove a high-frequency component.