firdecimator (firdecim)

The firdecim object family implements a basic interpolator with an integer output-to-input resampling ratio \(D\) . It is essentially just a firfilt object which operates on a block of samples at a time. An example of the firdecimator can be seen in [ref:fig-filter-firdecim-crcf] .

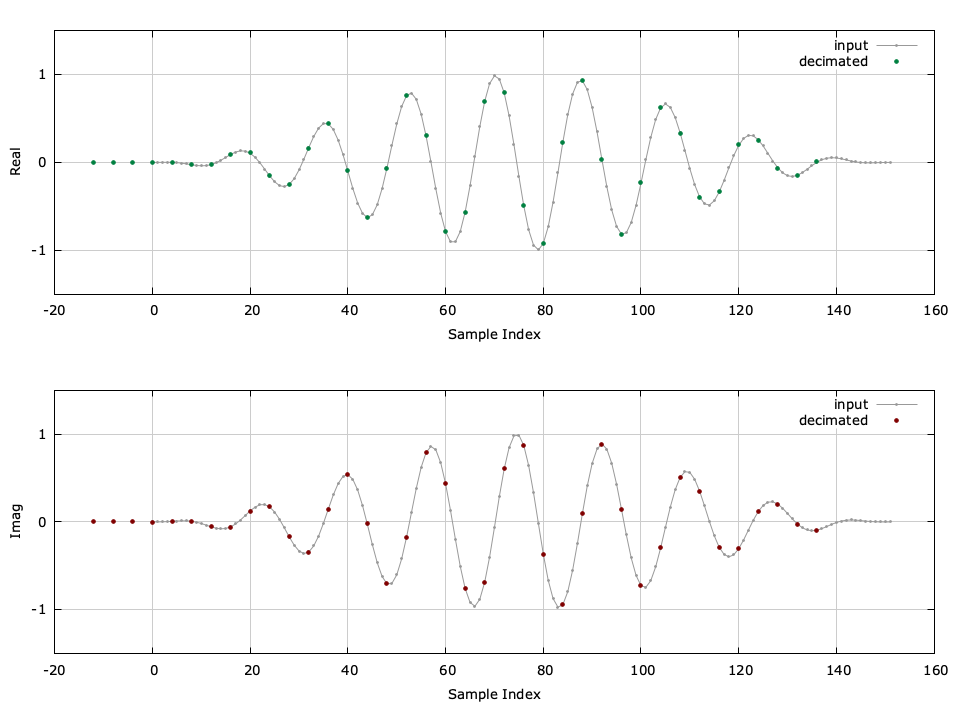
Figure [fig-filter-firdecim-crcf]. firdecim_crcf (firdecimator) example with \(D=4\) , compensating for filter delay.

Listed below is the full interface to the firdecim family of objects. While each method is listed for firdecim_crcf , the same functionality applies to firdecim_rrrf and firdecim_cccf .

• firdecim_crcf_create(D,*h,N) creates a firdecim object with a firdecimation factor \(D\) using \(N\) filter coefficients \(\vec{h}\) .
• firdecim_crcf_create_prototype(D,m,As) creates a firdecim object from a prototype filter with a firdecimation factor \(D\) , a delay of \(Dm\) samples, and a stop-band attenuation \(A_s\) dB.
• firdecim_crcf_create_rnyquist(type,D,m,beta,dt) creates a firdecim object from a square-root Nyquist prototype filter with a firdecimation factor \(D\) , a delay of \(Dm\) samples, an excess bandwidth factor \(\beta\) , and a fractional sample delay \(\Delta t\) (see [ref:section-filter-firdes-rnyquist] for details).
• firdecim_crcf_destroy(q) destroys a firdecim object, freeing all internally-allocated memory.
• firdecim_crcf_print(q) prints the parameters of a firdecim object to the standard output.
• firdecim_crcf_clear(q) clears the internal buffer of a firdecim object.
• firdecim_crcf_execute(q,*x,*y,k) computes the output firdecimation of the input sequence \(\vec{x}\) (which is \(D\) samples in size) at the index \(k\) and stores the result in \(y\) .

An example of the firdecim interface is listed below.

#include <liquid/liquid.h>

int main() {
    // options
    unsigned int M = 4;         // decimation factor
    unsigned int h_len = 21;    // filter length

    // design filter and create decimator object
    float h[h_len];             // filter coefficients
    firdecim_crcf q = firdecim_crcf_create(M,h,h_len);

    // generate input signal and decimate
    float complex x[M];         // input samples
    float complex y;            // output sample

    // run decimator (repeat as necessary)
    {
        firdecim_crcf_execute(q, x, &y);
    }

    // destroy decimator object
    firdecim_crcf_destroy(q);
}

A more detailed example is given in examples/firdecim_crcf_example.c in the main liquid project directory.