Symbol Synchronizer (symsync)
API Keywords: symsync symbol synchronizer timing recovery carrier recovery
The symsync object is a multi-rate symbol timing synchronizer useful for locking a received digital signal to the receiver's clock. It is effectively the same as the resamp object, but includes an internal control mechanism for tracking to timing phase and frequency offsets. The filter structure is a polyphase representation of a Nyquist matched filter. The instantaneous timing error is computed from the maximum likelihood timing error detector {cite:Mengali:1997} which relies on the derivative to the matched filter impulse response. liquid internally computes polyphase filter banks for both the matched and derivative-matched filters. If the output of the matched filter at sample \(k\) is \(y(k)\) and the output of the derivative matched filter is \(\dot{y}(k)\) then the instantaneous timing estimate is
$$ e_\tau(k) = \tanh\Bigl( y(k)\dot{y}(k) \Bigr) $$This timing error estimate has significant improvements over heuristic-based estimates such as the popular Mueller and Muller timing recovery scheme {cite:Mueller:1976}. Applying a simple first-order recursive loop filter yields the averaged timing estimate
$$ \Delta\tau(k) = \beta e_\tau(k) + \alpha\Delta\tau(k-1) $$where\(\alpha = 1-\omega_\tau\) and \(\beta = 0.22\omega_\tau\) are the loop filter coefficients for a given filter bandwidth\(\omega_\tau\) . While these coefficients are certainly not optimized, it is important to understand the difficulty in computing loop filter coefficients when a delay is introduced into a control loop. This delay is the result of the matched filter itself and can cause instability with traditional phase-locked loop filter designs. Internally the symsync object uses the principles of the resamp object (arbitrary resampler, see [ref:section-filter-resamp] ) for resampling the signal|actually decimating to one sample per symbol. Its internal control loop dynamically adjusts the rate \(r\) such that the timing phase of the receiver is aligned with the incoming signal's symbol timing.
Below is a code example demonstrating the symsync interface. Notice that the symsync_crcf_execute() method also returns the number of symbols written to the output buffer.
#include <liquid/liquid.h>
int main() {
// options
unsigned int k = 2; // samples/symbol
unsigned int m = 3; // filter delay (symbols)
float beta = 0.3f; // filter excess bandwidth factor
unsigned int npfb = 32; // number of polyphase filters in bank
int ftype = LIQUID_FIRFILT_RRC; // filter type
// create symbol synchronizer
symsync_crcf q = symsync_crcf_create_rnyquist(ftype,k,m,beta,npfb);
float complex * x; // complex input
float complex * y; // output buffer
unsigned int nx; // number of input samples
unsigned int num_written; // number of values written to buffer
// ... initialize input, output ...
// execute symbol synchronizer, storing result in output buffer
symsync_crcf_execute(q, x, nx, y, &num_written);
// ... repeat as necessary ...
// clean up allocated objects
symsync_crcf_destroy(q);
}
Listed below is the full interface to the symsync family of objects. While each method is listed for symsync_crcf , the same functionality applies to symsync_rrrf and symsync_cccf .
- symsync_crcf_create(k,N,*h,h_len) creates a symsync object from a prototype filter \(h\) of length\(h_{len}\) and having \(k\) samples per symbol. The internal object restructures the input filter into a polyphase prototype having \(N\) filters.
- symsync_crcf_create_rnyquist(ftype,k,m,beta,N) creates a symsync object from a square-root Nyquist prototype of type ftype (see [ref:section-filter-firdes-rnyquist] for a description of available square-root Nyquist filters in liquid). The generated filter has \(k\) samples per symbol, a nominal delay of \(m\) symbols, and an excess bandwidth factor of\(\beta\) . The internal polyphase filter bank has \(N\) filters.
- symsync_crcf_destroy(q) destroys the symbol synchronizer, freeing all internally-allocated memory.
- symsync_crcf_print(q) prints the internal properties of the symbol synchronizer object to the standard output.
- symsync_crcf_clear(q) resets the symbol synchronizer, clearing the internal buffers and filter state.
- symsync_crcf_set_lf_bw(q,w) sets the internal bandwidth of the loop filter to \(\omega\) .
- symsync_crcf_lock(q) locks the symbol synchronizer such that it will still decimate the incoming signal but will not update its internal state.
- symsync_crcf_unlock(q) unlocks the symbol synchronizer, resuming its ability to track to the input signal.
- symsync_crcf_execute(q,*x,nx,*y,*ny) executes the resampler for an input array \(\vec{x}\) with \(n_x\) samples, storing the resulting samples in the output array \(y\) specifying the number of samples written as \(n_y\) .
- symsync_crcf_get_tau(q) returns the current timing estimate (fractional sampling interval) of the object.
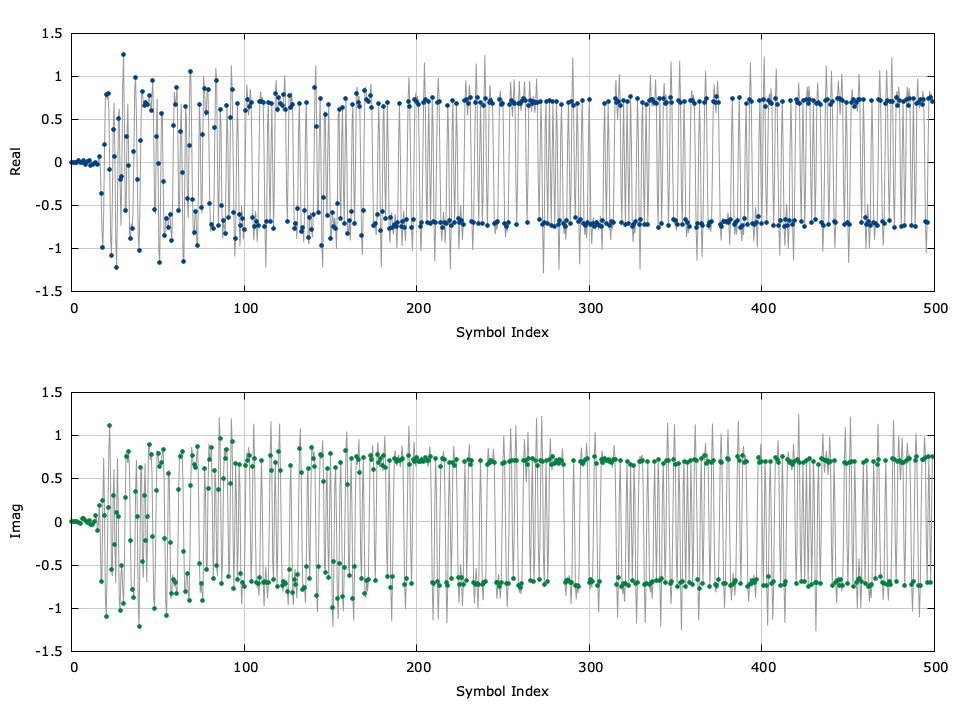
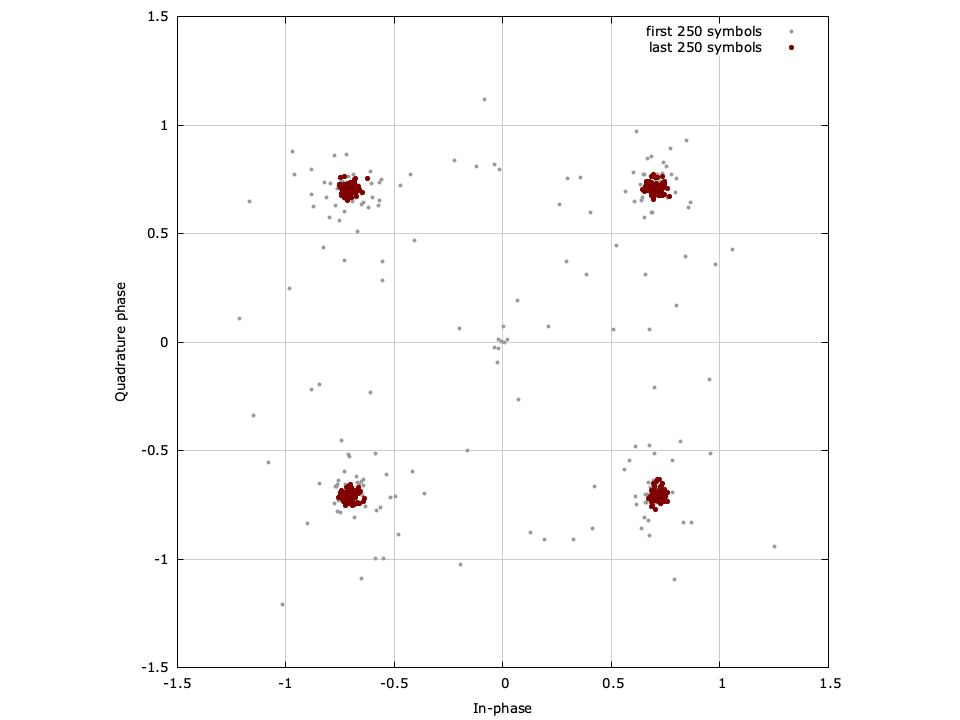
Figure [fig-filter-symsync]. symsync (symbol synchronizer) demonstration for a QPSK signal with a square-root raised-cosine pulse with \(k=2\) samples/symbol, a delay of \(m=4\) symbols, and an excess bandwidth factor \(\beta=0.3\)
[ref:fig-filter-symsync] demonstrates the symsync_crcf object recovering the sample timing phase for a QPSK signal. For a more detailed example, refer to examples/symsync_crcf_example.c located under the main liquid project source directory.