Half-band Filter/Resampler (resamp2)
API Keywords: resamp2 dyadic half-band resample two stage filter bank filterbank
resamp2 is a half-band resampler used for efficient interpolation and decimation. The internal filter of the resamp2 object is a Kaiser-windowed \(\sinc\) (see firdes_kaiser_window , [ref:section-filter-firdes] ) with\(f_c = 1/2\) . This makes the filter half-band, and puts the half-power (6 dB) cutoff point\(\omega_c\) at \(\pi/2\) (one quarter of the sampling frequency). In fact, any FIR filter design using a windowed \(\sinc\) function with periodicity \(f_c=1/2\) will generate a Nyquist half-band filter (zero inter-symbol interference). This is because {cite:Vaidyanathan:1993((4.6.3))}
$$ h(Mn) = \begin{cases} 1 & n=0 \\ 0 & \text{otherwise} \end{cases} $$which holds for \(h(n) = w(n) \sin(\pi n/M) / (\pi n)\) since\(\sin(\pi n/M) = 0\) for \(n=\) any non-zero multiple of M. Additionally, \(M=2\) is the special case of half-band filters. In particular half-band filtering is computationally efficient because half the coefficients of the filter are zero, and the remaining half are symmetric (so long as \(w(n)\) is also symmetric). In theory, this means that for a filter length of \(4m+1\) taps, only \(m\) computations are necessary {cite:harris:2004}. The resamp2 object in liquid uses a Kaiser window for \(w(n)\) for several reasons, but in particular because it is nearly optimum, and it is easy to trade side-lobe attenuation for transition bandwidth. Listed below is the full interface to the resamp2 family of objects. While each method is listed for resamp2_crcf , the same functionality applies to resamp2_rrrf and resamp2_cccf .
- resamp2_crcf_create(m,f0,As) creates a resamp2 object with a resampling rate 2, a filter semi-length of \(m\) samples (equivalent filter length \(4m+1\) ), centered at frequency \(f_0\) , and a stop-band suppression of \(A_s\) dB.
- resamp2_crcf_recreate(q,m,f0,As) recreates a resamp2 object with revised parameters.
- resamp2_crcf_destroy(q) destroys the resampler, freeing all internally-allocated memory.
- resamp2_crcf_print(q) prints the internal properties of the resampler to the standard output.
- resamp2_crcf_clear(q) clears the internal resampler buffers.
- resamp2_crcf_filter_execute(q,x,*y0,*y1) executes the resamp2 object as a half-band filter on an input sample \(x\) , storing the low-pass filter output in \(y_0\) and the high-pass filter output in \(y_1\) .
- resamp2_crcf_decim_execute(q,*x,*y) executes the half-band resampler as a decimator for an input array \(\vec{x}\) with two samples, storing the resulting samples in the array \(y\) .
- resamp2_crcf_interp_execute(q,x,*y) executes the half-band resampler as an interpolator for an input sample \(x\) , storing the resulting two output samples in the array \(\vec{y}\) .
Below is a code example demonstrating the resamp2 interface.
#include <liquid/liquid.h>
int main() {
// options
unsigned int m = 7; // filter semi-length
float As= 60.0f; // resampling filter stop-band attenuation
// create half-band resampler
resamp2_crcf q = resamp2_crcf_create(m,0.0f,As);
float complex x; // complex input
float complex y[2]; // output buffer
// ... initialize input ...
{
// execute half-band resampler as interpolator
resamp2_crcf_interp_execute(q, x, y);
}
// ... repeat as necessary ...
// clean up allocated objects
resamp2_crcf_destroy(q);
}
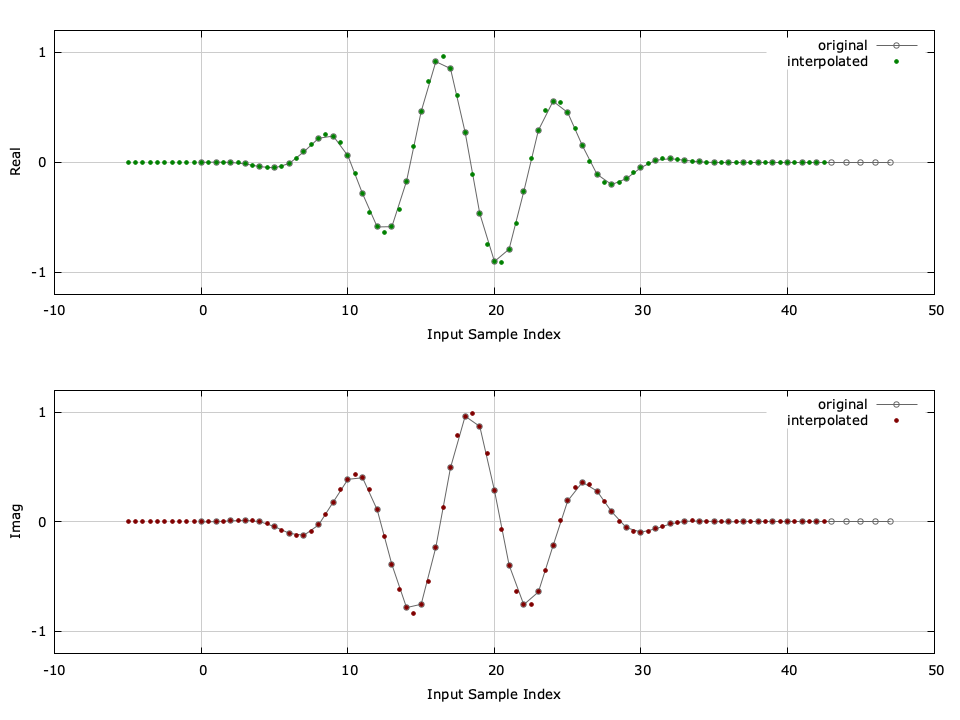
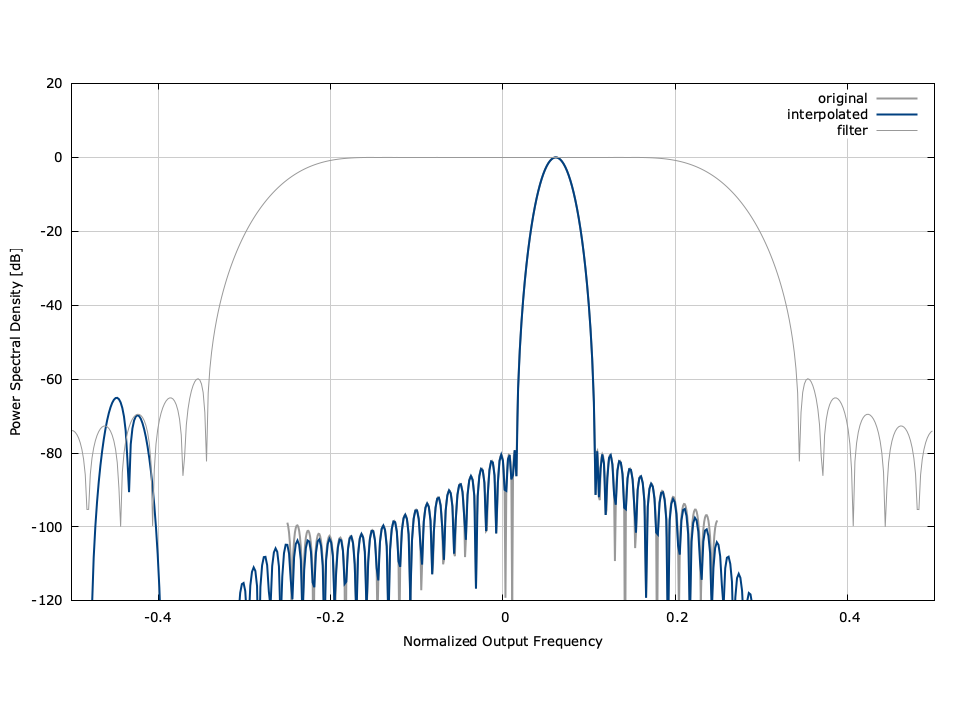
Figure [fig-filter-resamp2_crcf]. resamp2_crcf (half-band resampler) interpolator demonstration
[ref:fig-filter-resamp2_crcf] gives a graphical depiction in both the time and frequency domains of the half-band resampler acting as an interpolator. The time series has been aligned (shifted by the filter delay and scaled by the resampling rate) to show equivalence. For more detailed and extensive examples, refer to examples/resamp2_crcf_decim_example.c and examples/resamp2_crcf_interp_example.c located in the main liquid project source directory.