For arbitrary (e.g. irrational) resampling ratios, the resamp object is the ideal solution. It makes no restrictions on the output-to-input resampling ratio (e.g. irrational values are fair game). The arbitrary resampler uses a polyphase filter bank for interpolation between available input sample points.
Because the number of outputs for each input is not fixed, the interface needs some explaining. Over time the true resampling ratio will equal the value specified, however from one input to the next, the number of outputs will change. For example, if the resampling rate is \(2\) , every input will produce exactly two output samples. However, if the resampling rate is \(\sqrt{2} \approx 1.4142\) , an input sample will usually produce one output, but sometimes two. In the limit (on average ) however, the ratio of output samples to input samples will be exactly \(\sqrt{2}\) . The resamp object handles this internally by storing the accumulated sampling phase and produces an output for each overflow (i.e. values where the accumulated phase is equal to or exceeds 1).
Below is a code example demonstrating the resamp interface. Notice that the resamp_crcf_execute() method also returns the number of samples written to the buffer. This number will never exceed \(\lceil r \rceil\) .
#include <liquid/liquid.h>
int main() {
// options
unsigned int h_len = 13; // filter semi-length (filter delay)
float r=0.9f; // resampling rate (output/input)
float bw=0.5f; // resampling filter bandwidth
float slsl=-60.0f; // resampling filter sidelobe suppression level
unsigned int npfb=32; // number of filters in bank (timing resolution)
// create resampler
resamp_crcf q = resamp_crcf_create(r,h_len,bw,slsl,npfb);
unsigned int n = (unsigned int)ceilf(r);
float complex x; // complex input
float complex y[n]; // output buffer
unsigned int num_written; // number of values written to buffer
// ... initialize input ...
// execute resampler, storing result in output buffer
resamp_crcf_execute(q, x, y, &num_written);
// ... repeat as necessary ...
// clean up allocated objects
resamp_crcf_destroy(q);
}
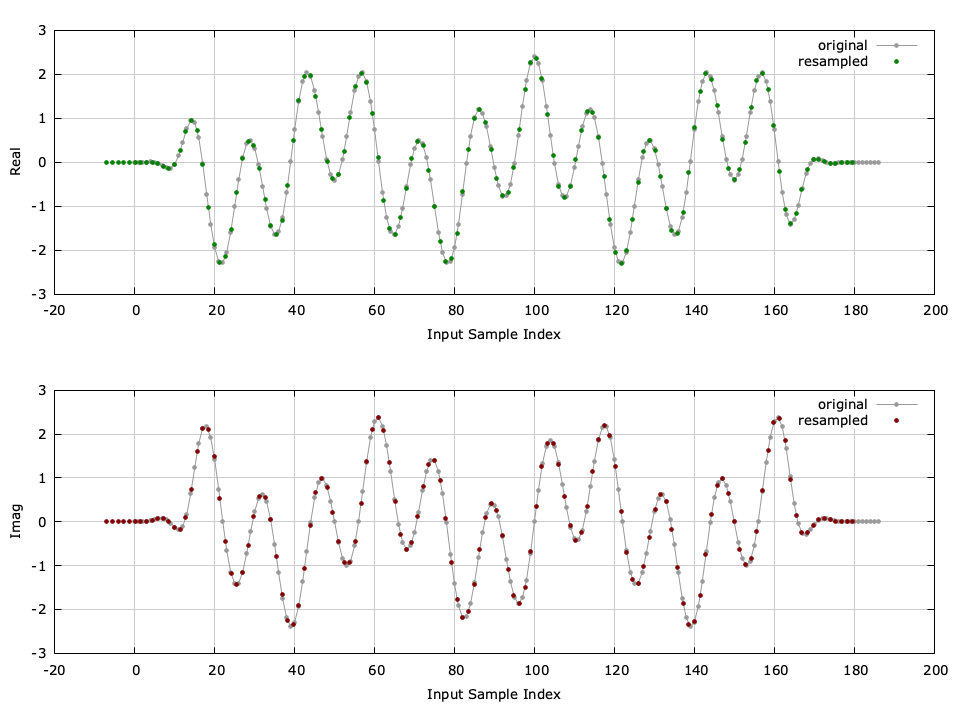
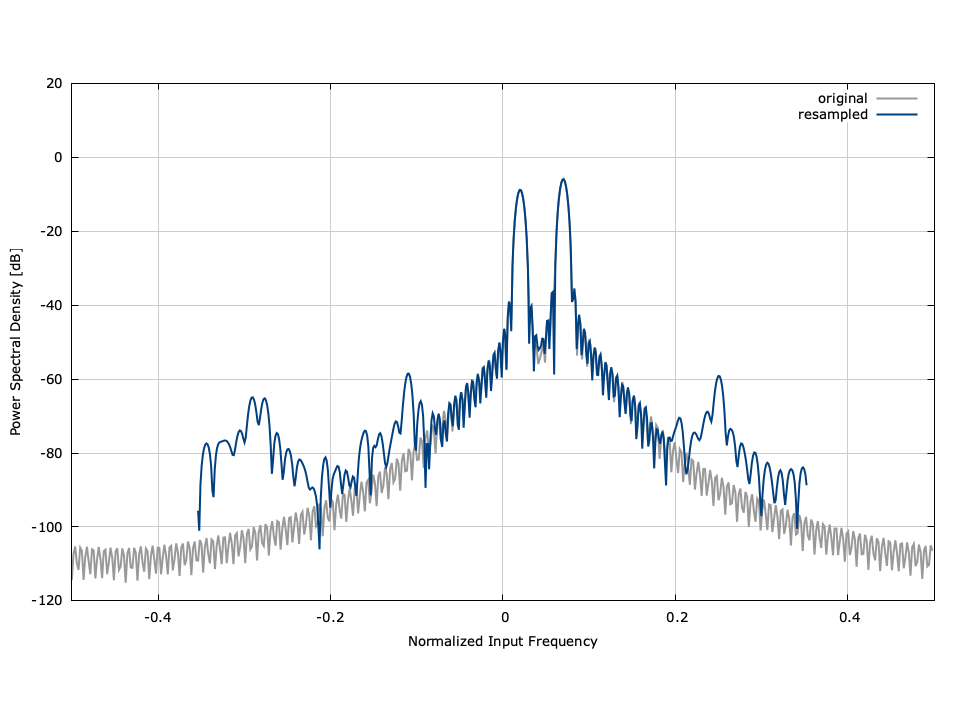
[ref:fig-filter-resamp_crcf] gives a graphical depiction of the arbitrary resampler, in both the time and frequency domains. The time series has been aligned (shifted by the filter delay and scaled by the resampling rate) to show equivalence. Additionally, the signal's power spectrum has been scaled by \(r\) to reflect the change in sampling rate. In the example the input array size is 187 samples; the resampler produced 133 output samples which yields a true resampling rate of \(\dot{r} = 133/187 \approx 0.71123\) which is close to the target rate of \(r = 1/\sqrt{2} \approx 0.70711\) .
It is important to understand how filter design impacts the performance of the resampler. The resamp object interpolates between available sample points to minimize aliasing effects on the output signal. This is apparent in the power spectral density plot in[ref:fig-filter-resamp_crcf] which shows very little aliasing on the output signal. Aliasing can be reduced by increasing the filter length at the cost of additional computational complexity; additionally the number of filters in the bank can be increased to improve timing resolution between samples. For synchronization of digital receivers, it is always good practice to precede the resampler with an anti-aliasing filter to remove out-of-band interference.
Listed below is the full interface to the resamp family of objects. While each method is listed for resamp_crcf , the same functionality applies to resamp_rrrf and resamp_cccf .
- resamp_crcf_create(r,m,fc,As,N) creates a resamp object with a resampling rate \(r\) , a nominal filter delay of \(m\) samples, a cutoff frequency of \(f_c\) , a stop-band suppression of \(A_s\) dB, using a polyphase filterbank with \(N\) filters.
- resamp_crcf_destroy(q) destroys the resampler, freeing all internally-allocated memory.
- resamp_crcf_print(q) prints the internal properties of the resampler to the standard output.
- resamp_crcf_reset(q) clears the internal resampler buffers.
- resamp_crcf_setrate(q,r) sets the resampling rate to \(r\) .
- resamp_crcf_execute(q,x,*y,*nw) executes the resampler for an input sample \(x\) , storing the resulting samples in the output array \(y\) specifying the number of samples written as \(n_w\) . The output buffer \(y\) needs to be at least \(\lceil r \rceil\) .
See also : resamp2 , firpfb , symsync , examples/resamp_crcf_example.c
Figure [fig-filter-resamp_crcf]. resamp_crcf (arbitrary resampler) demonstration, \(r = 1/\sqrt{2} \approx 0.7071\)