Quasi-Newton Search (qnsearch)
Keywords: Quasi-Newton search gradient descent search optimization
qnsearch (Quasi-Newton Search)∞
The qnsearch object in liquid implements the Quasi-Newton search algorithm which uses the first- and second-order derivatives (gradient vector and Hessian matrix) in its update equation. Newtonian-based search algorithms approximate the function to be nearly quadratic near its optimum which requires the second partial derivative (Hessian matrix) to be computed or estimated at each iteration. Quasi-Newton methods circumvent this by approximating the Hessian with successive gradient computations (or estimations) with each step. The Quasi-Newton method is usually faster than the gradient search due in part to its second-order (rather than a first-order) Taylor series expansion about the function of interest, however its update criteria is significantly more involved. In particular the step size must be sufficiently conditioned otherwise the algorithm can result in instability.
An example of the qnsearch interface is listed below. Notice that its interface is virtually identical to that of the gradsearch object.
#include <liquid/liquid.h>
int main() {
unsigned int num_parameters = 8; // search dimensionality
unsigned int num_iterations = 100; // number of iterations to run
float target_utility = 0.01f; // target utility
float optimum_vect[num_parameters];
// ...
// create qnsearch object
qnsearch q = qnsearch_create(NULL,
optimum_vect,
num_parameters,
&liquid_rosenbrock,
LIQUID_OPTIM_MINIMIZE);
// execute batch search
qnsearch_execute(q, num_iterations, target_utility);
// execute search one iteration at a time
unsigned int i;
for (i=0; i<num_iterations; i++)
qnsearch_step(q);
// clean it up
qnsearch_destroy(q);
}
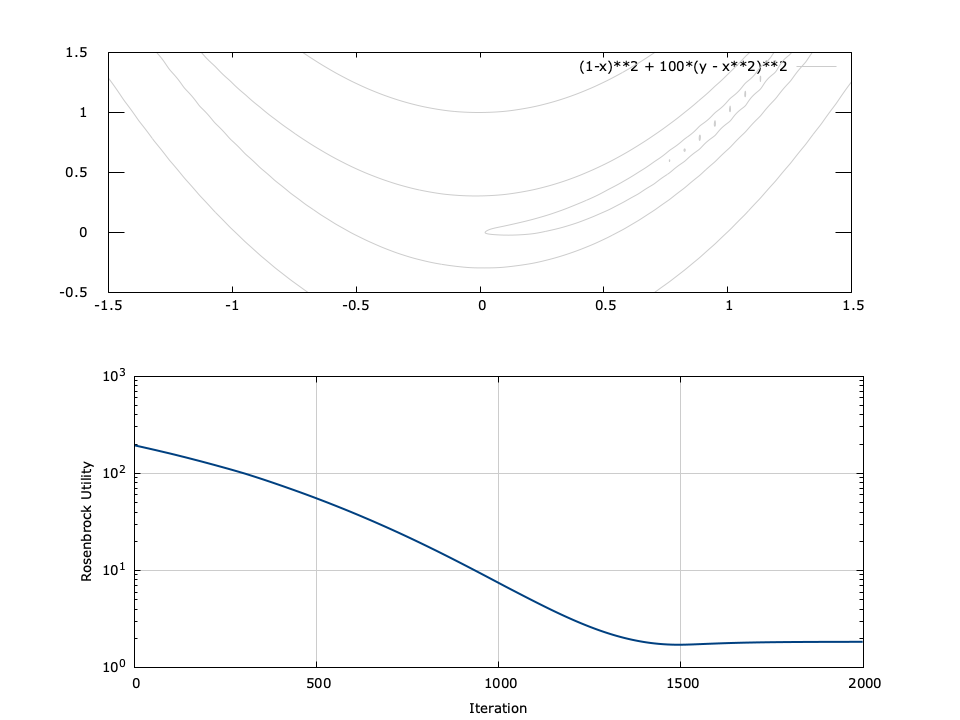
Figure [fig-optim-qnsearch]. qnsearch performance for 2-parameter Rosenbrock function \(f(x,y) = (1-x)^2 + 100(y-x^2)^2\) with a starting point of \((x_0,y_0)=(-0.1,1.4)\) . The minimum is located at \((1,1)\) .
[ref:fig-optim-qnsearch] depicts the performance of the gradient search for the Rosenbrock function, defined as\(f(x,y) = (1-x)^2 + 100(y-x^2)^2\) for input parameters \(x\) and \(y\) . The Rosenbrock function has a minimum at \((x,y)=(1,1)\) ; however the minimum lies in a deep valley which can be difficult to navigate. From the figure it is apparent that finding the valley is trivial, but convergence to the minimum is slow.