Infinite Impulse Response Filter Design (iirdes)
Keywords: infinite impulse response IIR filter design iirdes bilinear z-transform
liquid implements infinite impulse response (IIR) filter design for the five major classes of filters (Butterworth, Chebyshev type-I, Chebyshev type-II, elliptic, and Bessel) by first computing their analog low-pass prototypes, performing a bilinear\(z\) -transform to convert to the digital domain, then transforming to the appropriate band type (e.g. high pass) if necessary. Externally, the user may abstract the entire process by using the liquid_iirdes() method. Furthermore, if the end result is to create a filter object as opposed to computing the coefficients themselves, the iirfilt_crcf_create_prototype() method can be used to generate the object directly (see [ref:section-filter-iirfilt] ).
liquid_iirdes(), the simplified method∞
The liquid_iirdes() method designs an IIR filter's coefficients from one of the four major types (Butterworth, Chebyshev, elliptic/Cauer, and Bessel) with as minimal an interface as possible. The user specifies the filter prototype, order, cutoff frequency, and other parameters as well as the resulting filter structure (regular or second-order sections), and the function returns the appropriate filter coefficients that meet that design. Specifically, the interface is
liquid_iirdes(_ftype, _btype, _format, _n, _fc, _f0, _Ap, _As, *_B, *_A);
- _ftype is the analog filter prototype, e.g. LIQUID_IIRDES_BUTTER
- _btype is the band type, e.g. LIQUID_IIRDES_BANDPASS
- _format is the output format of the coefficients, e.g. LIQUID_IIRDES_SOS
- _n is the filter order
- _fc is the normalized cutoff frequency of the analog prototype
- _f0 is the normalized center frequency of the analog prototype (only applicable to bandpass and band-stop filter designs, ignored for low-pass and high-pass filter designs)
- _Ap is the pass-band ripple (only applicable to Chebyshev Type-I and elliptic filter designs, ignored for Butterworth, Chebyshev Type-II, and Bessel designs)
- _As is the stop-band ripple (only applicable to Chebyshev Type-II and elliptic filter designs, ignored for Butterworth, Chebyshev Type-I, and Bessel designs)
- _B , _A are the output feed-forward (numerator) and feed-back (denominator) coefficients, respectively. The format and size of these arrays depends on the value of the _format and _btype parameters. To compute the specific lengths of the arrays, first define the effective filter order \(N\) which is the same as the specified filter order for low- and high- pass filters, and doubled for band-pass and band-stop filters. If the the format is LIQUID_IIRDES_TF (the regular transfer function format) then the size of _B and _A is simply \(N\) . If, on the other hand, the format is LIQUID_IIRDES_SOS (second-order sections format) then a few extra steps are needed: define \(r\) as \(0\) when \(N\) is even and \(1\) when \(N\) is odd, and define \(L\) as \((N-r)/2\) . The sizes of _B and _A for the second-order sections case are each \(3(L+r)\) .
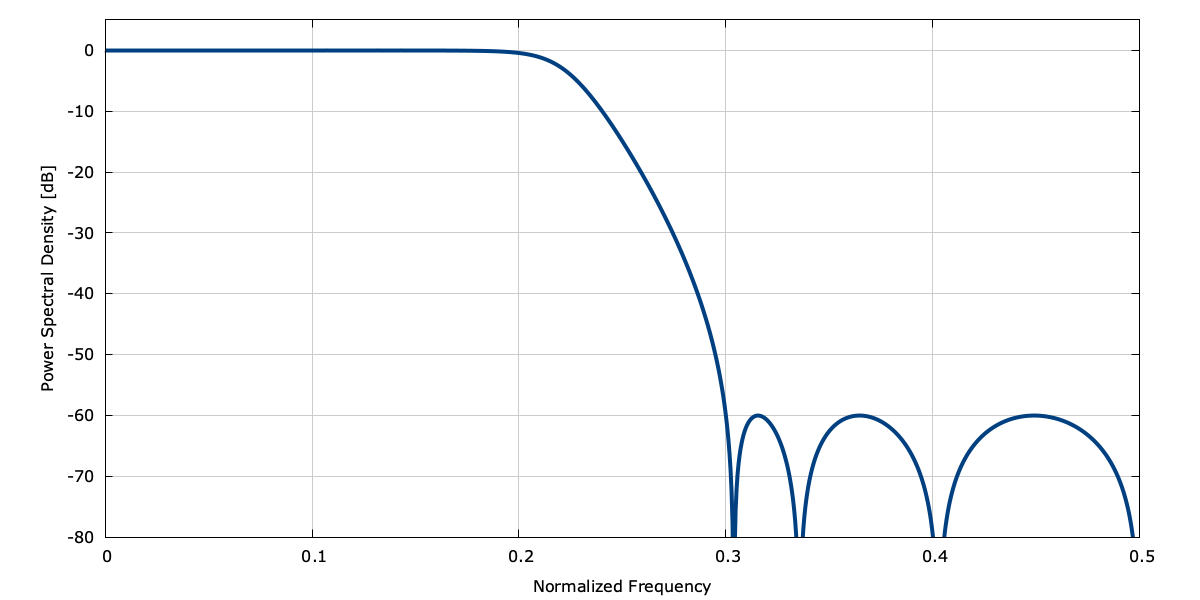
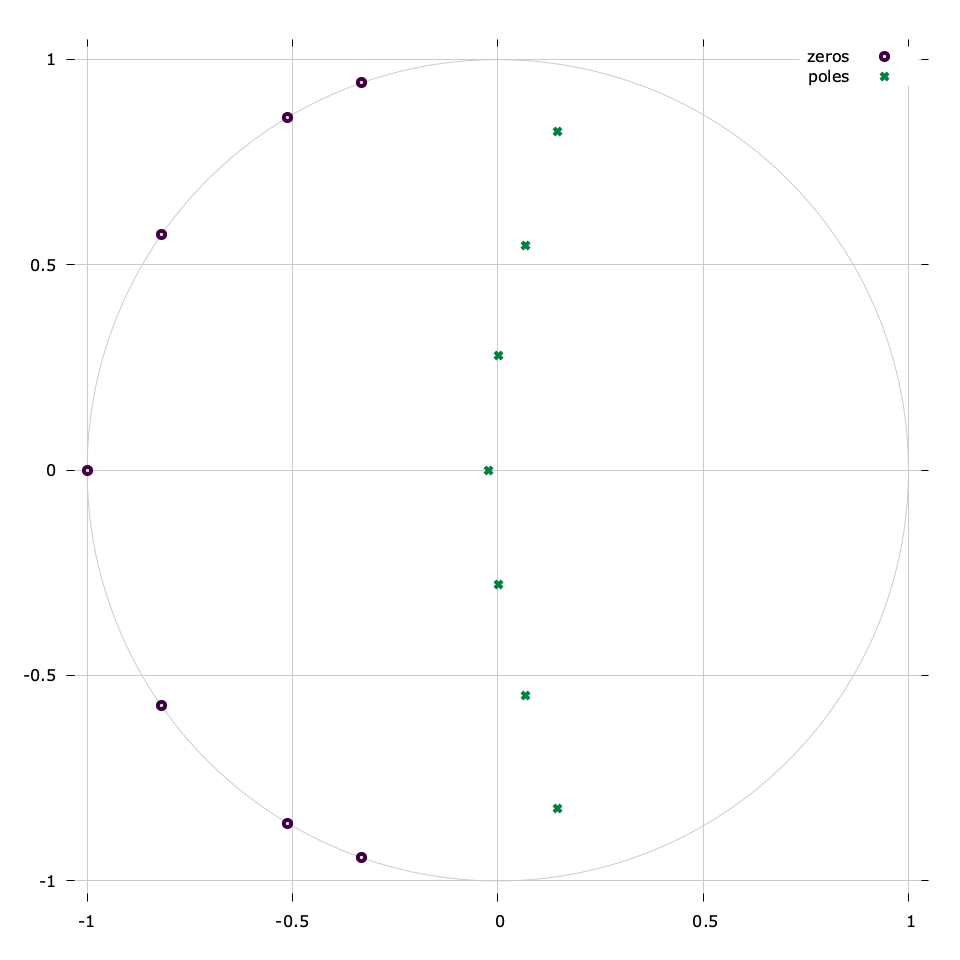
As an example, the following example designs a \(5^{th}\) -order elliptic band-pass filter with 1 dB ripple in the passband, 60 dB ripple in the stop-band, a cut-off frequency of \(f_c/F_s=0.2\) and a center frequency \(f_0/F_s=0.25\) ; the frequency response of the resulting filter can be found in[ref:fig-filter-iirdes_example] .
#include <liquid/liquid.h>
int main() {
// options
unsigned int order=5; // filter order
float fc = 0.20f; // cutoff frequency (low-pass prototype)
float f0 = 0.25f; // center frequency (band-pass, band-stop)
float As = 60.0f; // stopband attenuation [dB]
float Ap = 1.0f; // passband ripple [dB]
// derived values
unsigned int N = 2*order; // effective order (double because band-pass)
unsigned int r = N % 2; // odd/even order
unsigned int L = (N-r)/2; // filter semi-length
// filter coefficients arrays
float B[3*(L+r)];
float A[3*(L+r)];
// design filter
liquid_iirdes(LIQUID_IIRDES_ELLIP,
LIQUID_IIRDES_BANDPASS,
LIQUID_IIRDES_SOS,
order,
fc, f0, Ap, As,
B, A);
// print results
unsigned int i;
printf("B [%u x 3] :\n", L+r);
for (i=0; i<L+r; i++)
printf(" %12.8f %12.8f %12.8f\n", B[3*i+0], B[3*i+1], B[3*i+2]);
printf("A [%u x 3] :\n", L+r);
for (i=0; i<L+r; i++)
printf(" %12.8f %12.8f %12.8f\n", A[3*i+0], A[3*i+1], A[3*i+2]);
}
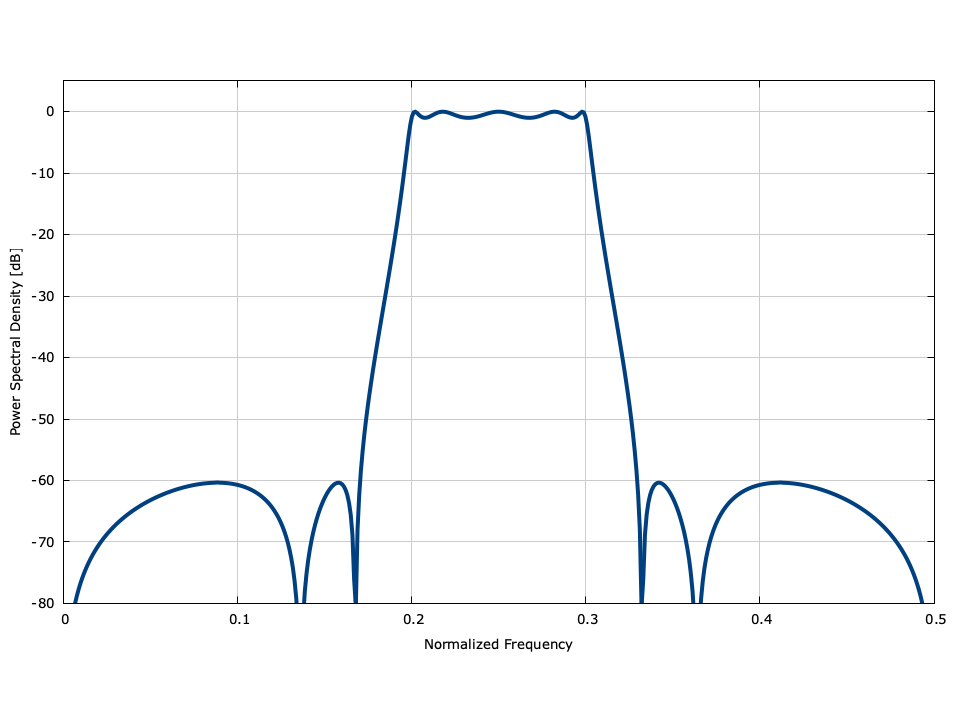
Figure [fig-filter-iirdes_example]. Example of the iirdes interface, designing a 5\(^{th}\) -order elliptic band-pass filter with 1 dB ripple in the passband, 60 dB ripple in the stop-band, a cut-off frequency of \(f_c/F_s=0.2\) and a center frequency \(f_0/F_s=0.25\)
internal description∞
While the user only needs to specify the filter parameters, the internal procedure for computing the coefficients is somewhat complicated. Listed below is the step-by-step process for liquid's IIR filter design procedure.
- Use butterf() , cheby1f() , cheby2f() , ellipf() , besself() to design a low-pass analog prototype \(H_a(s)\) in terms of complex zeros, poles, and gain. The azpkf extension stands for "analog zeros, poles, gain (floating-point)." - butter_azpkf() Butterworth (maximally flat in the pass-band) - cheby1_azpkf() Chebyshev Type-I (equiripple in the pass-band) - cheby2_azpkf() Chebyshev Type-II (equiripple in the stop-band) - ellip_azpkf() elliptic filter (equiripple in the pass- and stop-bands) - bessel_azpkf() Bessel (maximally flat group delay)
- Compute frequency pre-warping factor, \(m\) , to set cutoff frequency (and center frequency if designing a band-pass or band-stop filter) using the iirdes_freqprewarp() method.
- Convert the low-pass analog prototype \(H_a(s)\) to its digital equivalent \(H_d(z)\) (also in terms of zeros, poles, and gain) using the bilinear \(z\) -transform using the bilinear_zpkf() method. This maps the analog zeros/poles/gain into digital zeros/poles/gain.
- Transform the low-pass digital prototype to high-pass, band-pass, or band-stop using the iirdes_dzpk_lp2bp() method. For the band-pass and band-stop cases, the number of poles and zeros will need to be doubled. - LP low-pass filter : \(s = m (1+z^{-1}) / (1-z^{-1})\) - HP high-pass filter : \(s = m (1-z^{-1}) / (1+z^{-1})\) - BP band-pass filter : \(s = m (1-c_0 z^{-1}+z^{-2}) / (1-z^{-2})\) - BS band-stop filter : \(s = m (1-z^{-2}) / (1-c_0 z^{-1}+z^{-2})\)
- Transform the digital \(z/p/k\) form of the filter to one of the two forms: - TF typical transfer function for digital iir filters of the form\(B(z)/A(z)\) , iirdes_dzpk2tff() - SOS second-order sections form : \(\prod_k{ B_k(z)/A_k(z) }\) , iirdes_dzpk2sosf() . This is the preferred method.
A simplified example for this procedure is given in examples/iirdes_example.c .
Available Filter Types∞
There are currently five low-pass prototypes available for infinite impulse response filter design in liquid, as described below.
Butterworth∞
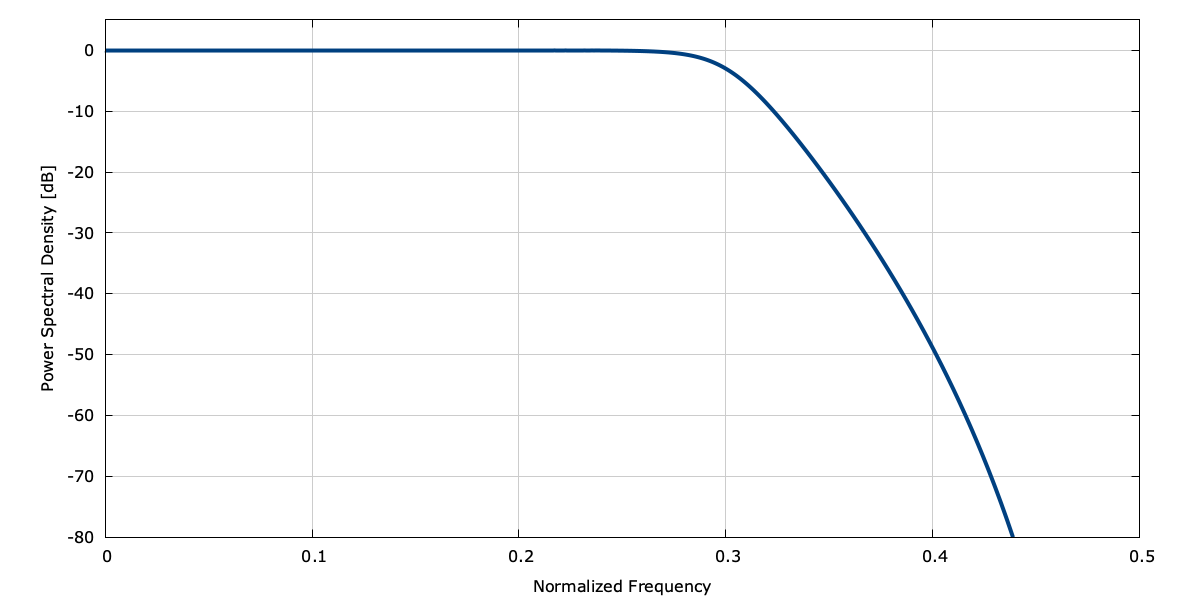
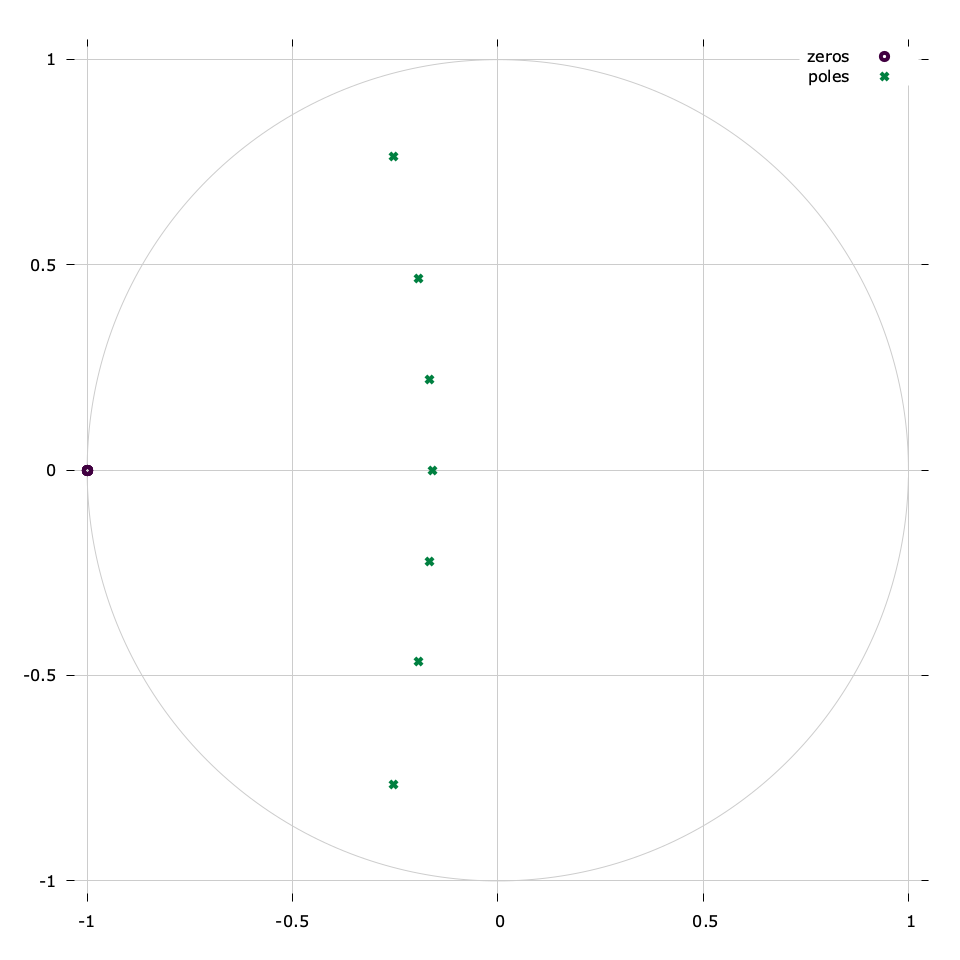
LIQUID_IIRDES_BUTTER is a Butterworth filter. This is an all-pole analog design that has a maximally flat magnitude response in the pass-band. The analog prototype interface is butter_azpkf() which computes the \(n\) complex roots \(p_{a0},p_{a1},\ldots,p_{an-1}\) of the \(n^{th}\) -order Butterworth polynomial,
$$ p_{ak} = \omega_c \exp\left\{ j \frac{\left(2k+n+1\right)\pi}{2n} \right\} $$for \(k=0,1,\ldots,n-1\) . Note that this results in a set of complex conjugate pairs such that\((-1)^n s_0 s_1 \cdots s_{n-1} = 1\) . An example of a digital filter response can be found in[ref:fig-filter-butter]
Chebyshev Type-I∞
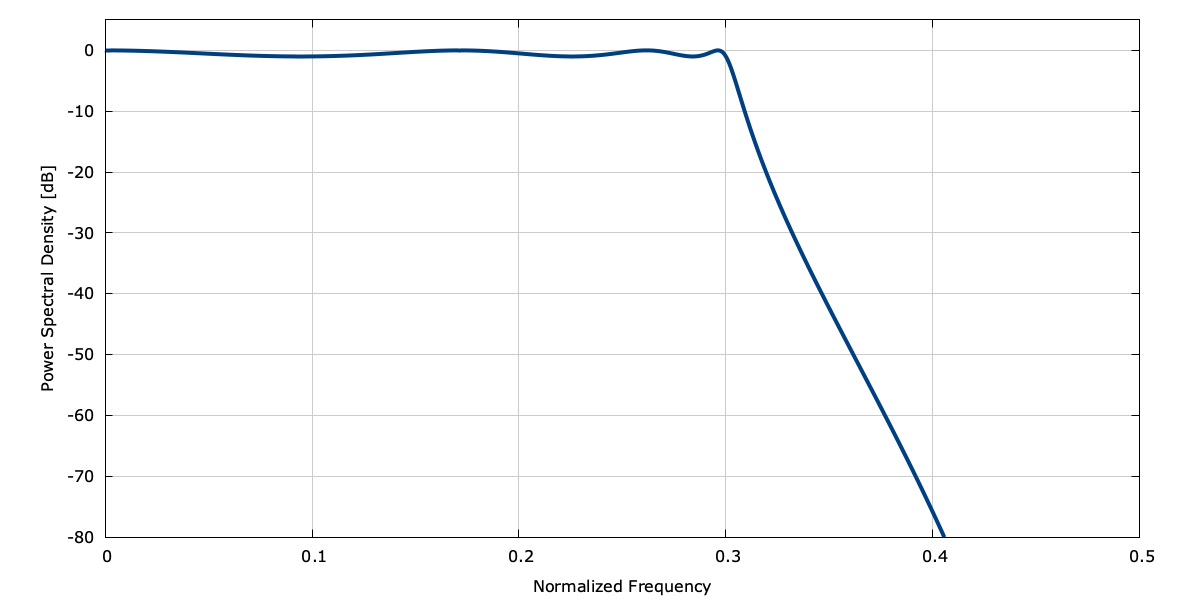
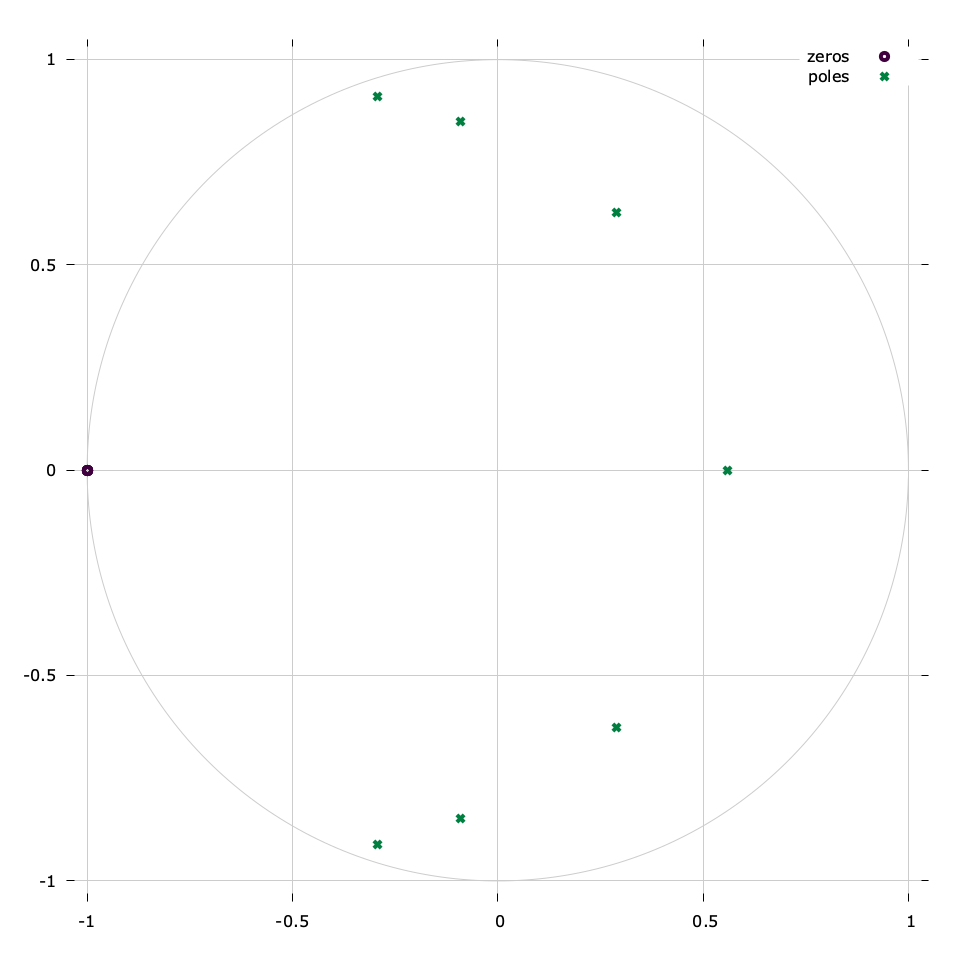
LIQUID_IIRDES_CHEBY1 is a Chebyshev Type-I filter. This design uses Chebyshev polynomials to create a filter with a sharper transition band than the Butterworth design by allowing ripples in the pass-band. The analog prototype interface is cheby1_azpkf() which computes the \(n\) complex roots \(p_{ak}\) of the \(n^{th}\) -order Chebyshev polynomial. An example of a digital filter response can be found in[ref:fig-filter-cheby1] .
Chebyshev Type-II∞
LIQUID_IIRDES_CHEBY2 is a Chebyshev Type-II filter. This design is similar to that of Chebyshev Type-I, except that the Chebyshev polynomial is inverted. This inverts the magnitude response of the filter and exhibits an equiripple behavior in the stop-band, rather than the pass-band. The analog prototype interface is cheby2_azpkf() . An example of a digital filter response can be found in[ref:fig-filter-cheby2]
Elliptical∞
LIQUID_IIRDES_ELLIP is an elliptic (Cauer) filter. This design allows ripples in both the pass-band and stop-bands to create a filter with a very sharp transition band. The design process is somewhat more involved than the Butterworth and Chebyshev prototypes and requires solving the elliptic integral of different moduli. For a more detailed description we refer the interested reader to {cite:Orfanidis:2006}. The analog prototype interface is ellip_azpkf() . An example of a digital filter response can be found in[ref:fig-filter-ellip] .
Bessel∞
LIQUID_IIRDES_BESSEL is a Bessel filter. This is an all-pole analog design that has a maximally flat group delay response (maximally linear phase response). The solution to the design happens to be the roots to the Bessel polynomials of equal order. Computing the roots to the polynomial is, again, somewhat complex. For a more detailed description we refer the interested reader to {cite:Orchard:1965}. The analog prototype interface is bessel_azpkf() . An example of a digital filter response can be found in[ref:fig-filter-bessel] .
bilinear_zpkf (Bilinear z-transform)∞
The bilinear \(z\) -transform converts an analog prototype to its digital counterpart. Given a continuous time analog transfer function in zeros/poles/gain form ("zpk") with \(n_z\) zeros and \(n_p\) poles
$$ H_a(s) = k_a \frac{ (s-z_{a0})(s-z_{a1})\cdots(s-z_{an_z-1}) }{ (s-p_{a0})(s-p_{a1})\cdots(s-p_{an_p-1}) } $$the bilinear \(z\) -transform converts \(H_a(s)\) into the discrete transfer function \(H_d(z)\) by mapping the \(s\) -plane onto the \(z\) -plane with the approximation
$$ s \approx \frac{2}{T} \frac{1-z^{-1}}{1 + z^{-1}} $$This maps \(H_a(0) \rightarrow H_d(0)\) and\(H_a(\infty) \rightarrow H_d(\omega_s/2)\) , however we are free to choose the pre-warping factor which maps the cutoff frequency \(\omega_c\) .
$$ s \rightarrow \omega_c \cot\left(\frac{\pi \omega_c}{\omega_s}\right) \frac{1-z^{-1}}{1+z^{-1}} $$Substituting this into \(H_a(s)\) gives the discrete-time transfer function
$$ H(z) = k_a \frac{ \left(m\frac{1-z^{-1}}{1+z^{-1}}-z_{a0}\right) \left(m\frac{1-z^{-1}}{1+z^{-1}}-z_{a1}\right) \cdots \left(m\frac{1-z^{-1}}{1+z^{-1}}-z_{an_z-1}\right) }{ \left(m\frac{1-z^{-1}}{1+z^{-1}}-p_{a0}\right) \left(m\frac{1-z^{-1}}{1+z^{-1}}-p_{a1}\right) \cdots \left(m\frac{1-z^{-1}}{1+z^{-1}}-p_{an_p-1}\right) } $$where \(m=\omega_c \cot\left(\pi \omega_c / \omega_s\right)\) is the frequency pre-warping factor, computed in liquid via the method iirdes_freqprewarp() . Multiplying both the numerator an denominator by \((1+z^{-1})^{n_p}\) and applying some algebraic manipulation results in the digital filter
$$ H_d(s) = k_d \frac{ (1-z_{d0}z^{-1})(1-z_{d1}z^{-1})\cdots(1-z_{dn-1}z^{-1}) }{ (1-p_{d0}z^{-1})(1-p_{d1}z^{-1})\cdots(1-p_{dn-1}z^{-1}) } $$The bilinear_zpk() method in liquid transforms the the analog zeros (\(z_{ak}\) ), poles (\(p_{ak}\) ), and gain (\(H_0\) ) into their digital equivalents (\(z_{dk}\) , \(p_{dk}\) , \(G_0\) ). For a filter with \(n_z\) analog zeros \(z_{ak}\) the digital zeros \(z_{dk}\) are computed as
$$ z_{dk} = \begin{cases} \frac{1 + m z_{ak}}{1 - m z_{ak}} & k \lt n_z \\ -1 & \text{otherwise} \end{cases} $$where \(m\) is the pre-warping factor. For a filter with \(n_p\) analog poles \(p_{ak}\) the digital poles \(p_{dk}\) are computed as
$$ p_{dk} = \frac{1 + m p_{ak}}{1 - m p_{ak}} $$Keeping in mind that an analog filter's order is defined by its number of poles, the digital gain can be computed as
$$ G_0 = H_0 \prod_{k=0}^{n_p-1}{ \frac{1 - p_{dk}}{1 - z_{dk}} } $$Filter transformations∞
The prototype low-pass digital filter can be converted into a high-pass, band-pass, or band-stop filter using a combination of the following filter transformations in liquid:
- iirdes_dzpk_lp2hp(*_zd,*_pd,_n,*_zdt,*_pdt) Converts a low-pass digital prototype \(H_d(z)\) to a high-pass prototype. This is accomplished by transforming the \(n\) zeros and poles (represented by the input arrays _zd and _pd ) into \(n\) transformed zeros and poles (represented by the output arrays _zdt and _pdt ).
- iirdes_dzpk_lp2bp(*_zd,*_pd,_n,*_zdt,*_pdt) Converts a low-pass digital prototype \(H_d(z)\) to a band-pass prototype. This is accomplished by transforming the \(n\) zeros and poles (represented by the input arrays _zd and _pd ) into \(2n\) transformed zeros and poles (represented by the output arrays _zdt and _pdt ).
Filter Coefficient Computation∞
The digital filter defined by [ref:eqn-filter-iirdes-Hd] can be expanded to fit the familiar IIR transfer function as in[ref:eqn-filter-iirfilt-Hz] . This can be accomplished using the iirdes_dzpk2tff() method. Alternatively, the filter can be written as a set of cascaded second-order IIR filters:
$$ H_d(z) = G_0 \left[ \frac{1 + z^{-1}} {1 - p_0 z^{-1}} \right]^r \prod_{k=1}^{L} {\left[ G_i \frac{(1-z_iz^{-1})(1-z_i^*z^{-1})} {(1-p_iz^{-1})(1-p_i^*z^{-1})} \right]} $$where \(r=0\) when the filter order is odd, \(r=1\) when the filter order is even, and \(L=(n-r)/2\) . This can be accomplished using the iirdes_dzpk2sosf() method and is preferred over the traditional transfer function design for stability reasons.