Finite Impulse Response Filter (firfilt)

Finite impulse response (FIR) filters are implemented in liquid with the firfilt family of objects. FIR filters (also known as non-recursive filters ) operate on discrete-time samples, computing the output \(y\) as the convolution of the input \(\vec{x}\) with the filter coefficients \(\vec{h}\) as

$$ y(n) = \sum_{k=0}^{N-1}{ h(k) x(N-k-1) } $$

where \(\vec{h} = [h(0),h(1),\ldots,h(N-1)]\) is the filter impulse response. Notice that the output sample in the above equation is simply the vector dot product (see dotprod ) of the filter coefficients \(\vec{h}\) with the time-reversed sequence\(\vec{x}\) .

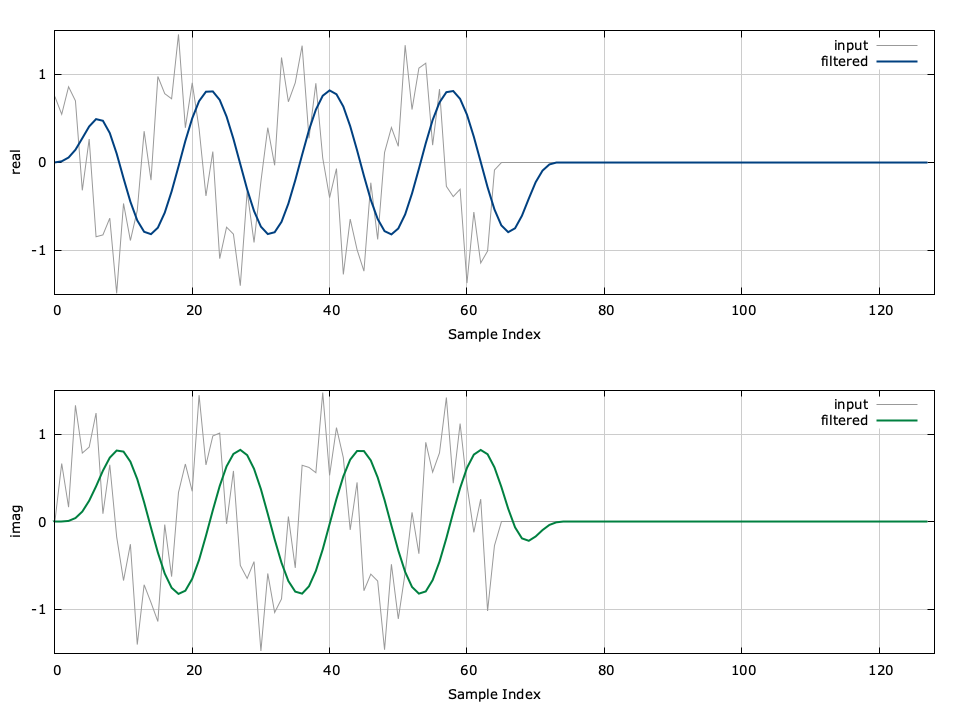
An example of the firfilt can be seen in[ref:fig-filter-firfilt_crcf] in which a low-pass filter is applied to a signal to remove a high-frequency component. An example of the firfilt interface is listed below.

#include <liquid/liquid.h>

int main() {
    // options
    unsigned int h_len=21;  // filter order
    float h[h_len];         // filter coefficients

    // ... initialize filter coefficients ...

    // create filter object
    firfilt_crcf q = firfilt_crcf_create(h,h_len);

    float complex x;    // input sample
    float complex y;    // output sample

    // execute filter (repeat as necessary)
    {
        firfilt_crcf_push(q, x);    // push input sample
        firfilt_crcf_execute(q,&y); // compute output
    }

    // destroy filter object
    firfilt_crcf_destroy(q);
}

The full list of interfaces to the firfilt family of objects can be found in its API page .