Forward Error-Correction (fec)
Keywords: forward error correction coding FEC encode decode convolutional Reed-Solomon Golay Viterbi Hamming SEC-DED CRC soft log likelihood ratio LLR
The fec module implements a set of forward error-correction codes for ensuring and validating data integrity through a noisy channel. Redundant "parity" bits are added to a data sequence to help correct errors introduced by the channel. The number of correctable errors depends on the number of parity bits of the coding scheme, which in turn affects its rate (efficiency). The fec object realizes forward error-correction capabilities in liquid while the methods checksum() and crc32() strictly implement error detection. Certain FEC schemes are only available to liquid by installing the external libfec library {cite:libfec:web}, available as a free download. A few low-rate (and fairly low efficiency) codes are available internally.
For conveniently combining forward error-correction coding with linear modulation , use the qpacketmodem object.
Hamming codes∞
Hamming codes are a specific type of block code which use parity bits capable of correcting one bit error in the block. With the addition of an extra parity bit, they are able to detect up to two errors, but are still only able to correct one. liquid implements the Hamming(7,4), Hamming(8,4), and Hamming(12,8) codes. The Hamming(8,4) can detect one additional error over the Hamming(7,4) code; however at the time of writing this document the number of detected errors is not passed to the user so the Hamming(8,4) code is effectively the same as Hamming(7,4) but with a lower rate. Additionally, liquid implements the Hamming(12,8) code which accepts an 8-bit symbol and adds four parity bits, extending it to a 12-bit symbol. This yields a theoretical rate of \(2/3\) , and actually has a performance very similar to that of the Hamming(7,4) code, even with a higher rate.
Simple Repeat Codes∞
The rep3 code is a simple repeat code which simply repeats the message twice (transmits it three times). The decoder takes a majority vote of the bits received by applying a simple series bit masks. If the original bit is represented as \(s\) , then the transmitted bits are\(s s s\) . Let the received bit sequence be \(r_0 r_1 r_2\) . The estimated transmitted bit is 0 if the sum of the received bits is less than 2, and 1 otherwise. This is equivalent to
$$ \hat{s} = (r_0 \land r_1) + (r_0 \land r_2) + (r_1 \land r_2) $$where \(+\) represents logical or and \(\land\) represents logical and . An error is detected if
$$ \hat{e} = (r_0 \oplus r_1) + (r_0 \oplus r_2) + (r_1 \oplus r_2) $$where \(\oplus\) represents logical exclusive or . In this fashion it is easy to decode several bytes of data at a time because machine architectures have low-level bit-wise manipulation instructions which can compute logical exclusive or and or very quickly. This is precisely how liquid decodes rep3 data, only in this case,\(s\) , \(r_0\) , \(r_1\) , and \(r_2\) represent a bytes of data rather than bits.
The rep5 code operates similarly, except that it transmits five copies of the original data sequence, rather than just three. The decoder takes the five received bits \(r_0,\ldots,r_4\) and adds (modulo 2) the logical and of every combination of three bits, viz
$$ \hat{s} = \sum_{i\ne j \ne k} {(r_i \land r_j \land r_k)} $$This roughly doubles the number of clock cycles to decode over rep3 .
It is well-known that repeat codes do not have strong error-correction capabilities for their rate, are are located far from the Shannon capacity bound {cite:Proakis:2001}. They are exceptionally weak relative to convolutional Viterbi and Reed-Solomon codes. However, their simplicity in implementation and low computational complexity gains them a place in digital communications, particularly in software radios where spectral efficiency goals might be secondary to processing constraints.
Golay(24,12) block code∞
The Golay(24,12) code is a \(1/2\) -rate block code which is capable of correcting up to three errors and detecting up to four. In truth, the Golay(24,12) code is an extension of the Golay(23,12) "perfect" code by adding an extra parity bit {cite:Lin:2004(Section 4.6)}. Specifically, the generator and parity check matrices are constructed systematically from a \(12 \times 12\) matrix \(\vec{P}\) as
$$ \vec{P} = \begin{bmatrix} 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 & 1 & 0 & 1 & 1 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 \\ 0 & 1 & 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 & 1 \\ 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 \\ \end{bmatrix} $$The generator matrix is simply\(\vec{G} = \left[ \vec{P}^T \,\,\, \vec{I}_{12} \right]\) and the parity check matrix is\(\vec{H} = \left[ \vec{I}_{12} \,\,\, \vec{P} \right]\) . Notice that \(\vec{P}^T = \vec{P}\) ; this plays an important role in systematic decoding {cite:Berlekamp:1972}.
SEC-DED block codes∞
The SEC-DED\((n,k)\) codes implement a certain class of "single error correction, double error detection" block codes. For the SEC-DED codes implemented in liquid , \(n\) can be represented by an integer \(m\) such that \(n=2^m\) and \(k = n + m + 2\) . Encoding and decoding begins with the \((n-k) \times n\) matrix \(\vec{P}\) such that the generator matrix is simply\(\vec{G} = \left[ \vec{I}_{n} \,\,\, \vec{P}^T \right]\) and the parity check matrix is\(\vec{H} = \left[ \vec{P} \,\,\, \vec{I}_{n-k} \right]\) . Decoding can be achieved by computing the syndrome vector and then using a look-up table to determine the location of the error. If the computed syndrome cannot be associated with any particular error location then multiple errors must have occurred for which the code cannot correct. There is currently no soft decoding implemented in liquid for the SEC-DED codes.
SEC-DED(22,16) block code∞
Encoding and decoding begins with the \(6 \times 16\) matrix \(\vec{P}\) as
$$ \vec{P}_{(22,16)} = \begin{bmatrix} {\tt 1001} & {\tt 1001} & {\tt 0011} & {\tt 1100} \\ {\tt 0011} & {\tt 1110} & {\tt 1000} & {\tt 1010} \\ {\tt 1110} & {\tt 1110} & {\tt 0110} & {\tt 0000} \\ {\tt 1110} & {\tt 0001} & {\tt 1101} & {\tt 0001} \\ {\tt 0001} & {\tt 0011} & {\tt 1100} & {\tt 0111} \\ {\tt 0100} & {\tt 0100} & {\tt 0011} & {\tt 1111} \\ \end{bmatrix} $$SEC-DED(39,32) block code∞
Encoding and decoding begins with the \(7 \times 32\) matrix \(\vec{P}\) as
$$ \vec{P}_{(39,32)} = \begin{bmatrix} {\tt 10001010} & {\tt 10000010} & {\tt 00001111} & {\tt 00011011} \\ {\tt 00010000} & {\tt 00011111} & {\tt 01110001} & {\tt 01100001} \\ {\tt 00010110} & {\tt 11110000} & {\tt 10010010} & {\tt 10100110} \\ {\tt 11111111} & {\tt 00000001} & {\tt 10100100} & {\tt 01000100} \\ {\tt 01101100} & {\tt 11111111} & {\tt 00001000} & {\tt 00001000} \\ {\tt 00100001} & {\tt 00100100} & {\tt 11111111} & {\tt 10010000} \\ {\tt 11000001} & {\tt 01001000} & {\tt 01000000} & {\tt 11111111} \\ \end{bmatrix} $$SEC-DEC(72,64) block code∞
The SEC-DED(72,64) code is a \(8/9\) -rate block code. Encoding and decoding begins with the \(8 \times 64\) matrix \(\vec{P}\) as
$$ \vec{P}_{(72,64)} = \begin{bmatrix} {\tt 11111111} & {\tt 00001111} & {\tt 00001111} & {\tt 00001100} & {\tt 01101000} & {\tt 10001000} & {\tt 10001000} & {\tt 10000000} \\ {\tt 11110000} & {\tt 11111111} & {\tt 00000000} & {\tt 11110011} & {\tt 01100100} & {\tt 01000100} & {\tt 01000100} & {\tt 01000000} \\ {\tt 00110000} & {\tt 11110000} & {\tt 11111111} & {\tt 00001111} & {\tt 00000010} & {\tt 00100010} & {\tt 00100010} & {\tt 00100110} \\ {\tt 11001111} & {\tt 00000000} & {\tt 11110000} & {\tt 11111111} & {\tt 00000001} & {\tt 00010001} & {\tt 00010001} & {\tt 00010110} \\ {\tt 01101000} & {\tt 10001000} & {\tt 10001000} & {\tt 10000000} & {\tt 11111111} & {\tt 00001111} & {\tt 00000000} & {\tt 11110011} \\ {\tt 01100100} & {\tt 01000100} & {\tt 01000100} & {\tt 01000000} & {\tt 11110000} & {\tt 11111111} & {\tt 00001111} & {\tt 00001100} \\ {\tt 00000010} & {\tt 00100010} & {\tt 00100010} & {\tt 00100110} & {\tt 11001111} & {\tt 00000000} & {\tt 11111111} & {\tt 00001111} \\ {\tt 00000001} & {\tt 00010001} & {\tt 00010001} & {\tt 00010110} & {\tt 00110000} & {\tt 11110000} & {\tt 11110000} & {\tt 11111111} \\ \end{bmatrix} $$Convolutional and Reed-Solomon codes∞
liquid takes advantage of convolutional and Reed-Solomon codes defined in libfec {cite:libfec:web}. These codes have much stronger error-correction capabilities than rep3 , rep5 , h74 , h84 , and h128 but are also much more computationally intensive to the host processor. liquid uses the rate \(1/2 (K=7)\) , \(1/2 (K=9)\) , \(1/3 (K=9)\) , and\(r1/6 (K=15)\) codes defined in libfec , but extends the two half-rate codes to punctured codes. These punctured codes (also known as "perforated" codes) are not as strong and cannot correct as many errors, but are more efficient and use less overhead than their half-rate counterparts. The 8-bit Reed-Solomon code is a (255,223) block code, also defined in libfec . Nominally, the scheme accepts 223 bytes (8-bit symbols) and adds 32 parity symbols to form a 255-symbol encoded block. libfec is an external library that liquid will leverage if installed, but will still compile otherwise (see [ref:section-buildguide] for details).
Interface∞
In designing the fec interface, I have tried to keep simplicity and reconfigurability in mind. The various forward error-correction schemes accept bits or symbols formatted in different lengths and have vastly different interfaces. This potentially makes switching from one scheme to another difficult as one needs to restructure the data accordingly. liquid takes care of all this formatting under the hood; regardless of the scheme used, the fec object accepts a block of uncoded data bytes and encodes them into an output block of coded data bytes.
- fec_create(scheme,*opts) creates a fec object of a specific scheme (see [ref:tab-fec-codecs] for available codecs). Notice that the length of the input message does not need to be specified until encode() or decode() is invoked. The opts argument is intended for future development and should be ignored by passing the NULL pointer (see example below).
- fec_recreate(q,scheme,*opts) recreates an existing fec object with a different scheme.
- fec_destroy(q) destroys a fec object, freeing all internally-allocated memory arrays.
- fec_encode(q,n,*msg_dec,*msg_enc) runs the error-correction encoder scheme on an \(n\) -byte input data array msg_dec , storing the result in the output array msg_enc . To obtain the length of the output array necessary, use the fec_get_enc_msg_length() method.
- fec_decode(q,n,*msg_enc,*msg_dec) runs the error-correction decoder on an input array msg_enc of \(k\) encoded bytes. The resulting best-effort decoded message is written to the \(n\) -byte output array msg_dec , allocated by the user. Notice that like the fec_encode() method, the input length\(n\) refers to the decoded message length. Depending upon the error-correction capabilities of the scheme, the resulting data might have been corrupted, and therefore it is recommended to use either a checksum or a cyclic redundancy check ([ref:fec-crc] ) to validate data integrity.
- fec_get_enc_msg_length(scheme,n) returns the length \(k\) of the encoded message in bytes for an uncoded input of \(n\) bytes using the specified encoding scheme. This method can be called before the fec object is created and is useful for allocating initial memory arrays.
Listed below is a simple example demonstrating the basic interface to the fec encoder/decoder object:
#include <liquid/liquid.h>
int main() {
unsigned int n = 64; // decoded message length (bytes)
fec_scheme fs = LIQUID_FEC_HAMMING74; // error-correcting scheme
// compute encoded message length
unsigned int k = fec_get_enc_msg_length(fs, n);
// allocate memory for data arrays
unsigned char msg_org[n]; // original message
unsigned char msg_enc[k]; // encoded message
unsigned char msg_rec[k]; // received message
unsigned char msg_dec[n]; // decoded message
// create fec objects
fec encoder = fec_create(fs,NULL);
fec decoder = fec_create(fs,NULL);
// repeat as necessary
{
// ... initialize message ...
// encode message
fec_encode(encoder, n, msg_org, msg_enc);
// ... push through channel ...
// decode message
fec_decode(decoder, n, msg_rec, msg_dec);
}
// clean up objects
fec_destroy(encoder);
fec_destroy(decoder);
return 0;
}
For a more detailed example demonstrating the full capabilities of the fec object, see examples/fec_example.c .
Soft Decoding∞
liquid supports soft decoding of most error-correcting schemes (with the exception of the Golay, SEC-DED, and Reed-Solomon codes). Soft decoding for all codes requires the log-likelihood ratio (LLR) output of the demodulator which can be achieved with the appropriate call: modem_demodulate_soft() (see [ref:section-modem-digital-soft] for details). The performance improvement for soft decoding varies for both the modulation and FEC scheme used; however in general one can expect to see an improvement of approximately 1.5 dB \(E_b/N_0\) over hard-decision decoding.
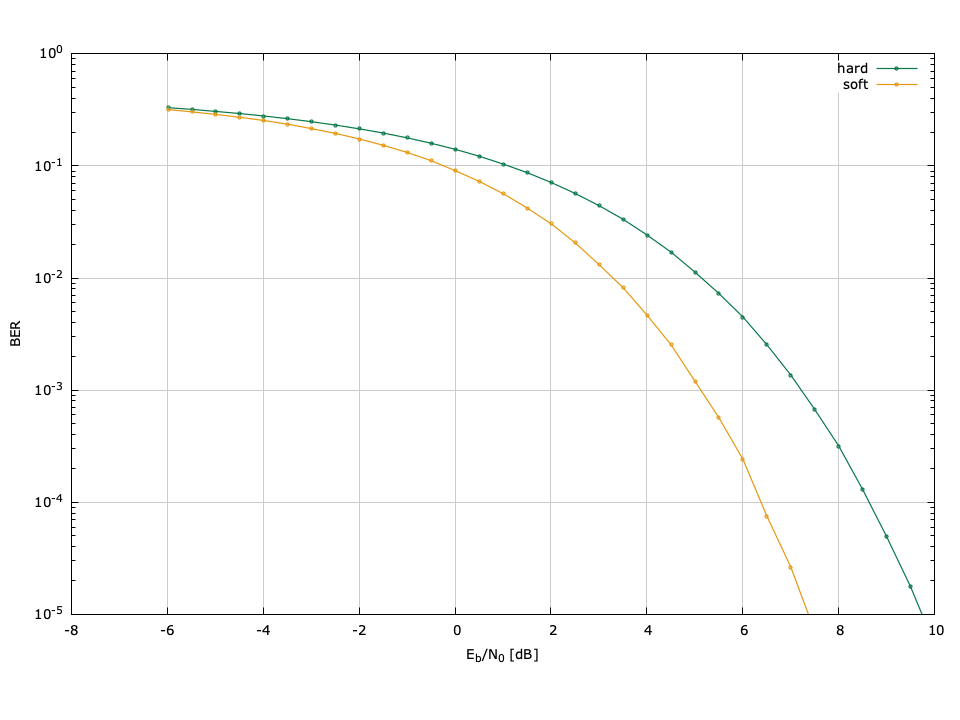
Figure [fig-fec-hardsoft_ber]. Bit error-rate performance for the Hamming(8,4) codec comparing hard-decision to soft-decision decoding.
[ref:fig-fec-hardsoft_ber] shows the performance improvement of using soft-decision vs. hard-decision decoding for the Hamming(8,4) block code.
Performance∞
The performance of an error-correction scheme is typically measured in the bit error rate (BER) for an antipodally modulated signal in the presence of additive white Gauss noise (AWGN). Certain applications prefer measuring performance in terms of the signal energy while others require bit energy, all relative to the noise variance. The two are related by
$$ \frac{E_b}{N_0} = \frac{E_s}{r N_0} $$where\(E_s\) is the signal energy,\(E_b\) is the bit energy,\(N_0\) is the noise energy, and\(r\) is the rate of the modulation and coding scheme pair, measured in bits/s/Hz.
Table [tab-fec-codecs]. Forward error-correction codecs available in liquid with \(E_b/N_0\) required for a BER of \(10^{-5}\)
| Built-in Block Codes | rate | hard | soft | description |
| LIQUID_FEC_UNKNOWN | - | - | - | unknown/unsupported scheme |
| LIQUID_FEC_NONE | 1 | 9.59 | 9.59 | no error-correction |
| LIQUID_FEC_REP3 | 1/3 | 11.08 | 9.56 | simple repeat code |
| LIQUID_FEC_REP5 | 1/5 | 11.39 | 9.64 | simple repeat code |
| LIQUID_FEC_HAMMING74 | 4/7 | 9.15 | 7.79 | Hamming (7,4) block code |
| LIQUID_FEC_HAMMING84 | 1/2 | 9.63 | 7.38 | Hamming (7,4) with extra parity bit |
| LIQUID_FEC_HAMMING128 | 2/3 | 8.82 | 8.13 | Hamming (12,8) block code |
| LIQUID_FEC_GOLAY2412 | 1/2 | 7.46 | - | Golay (24,12) block code |
| LIQUID_FEC_SECDED2216 | 2/3 | 8.84 | - | SEC-DED (22,16) block code |
| LIQUID_FEC_SECDED3932 | 4/5 | 8.29 | - | SEC-DED (39,32) block code |
| LIQUID_FEC_SECDED7264 | 8/9 | 8.05 | - | SEC-DED (72,64) block code |
| Convolutional Codes (Unpunctured) | ||||
| LIQUID_FEC_CONV_V27 | 1/2 | 6.44 | 4.29 | \(K=7\) , \(d_{free}=10\) |
| LIQUID_FEC_CONV_V29 | 1/2 | 5.79 | 3.78 | \(K=9\) , \(d_{free}=12\) |
| LIQUID_FEC_CONV_V39 | 1/3 | 5.41 | 3.59 | \(K=9\) , \(d_{free}=18\) |
| LIQUID_FEC_CONV_V615 | 1/6 | 3.81 | 2.00 | \(K=15\) , \(d_{free}\leq57\) (Heller 1968) |
| Convolutional Codes (Punctured) | ||||
| LIQUID_FEC_CONV_V27P23 | 2/3 | 6.86 | 4.65 | \(K=7\) , \(d_{free}=6\) |
| LIQUID_FEC_CONV_V27P34 | 3/4 | 7.33 | 5.29 | \(K=7\) , \(d_{free}=5\) |
| LIQUID_FEC_CONV_V27P45 | 4/5 | 7.73 | 5.50 | \(K=7\) , \(d_{free}=4\) |
| LIQUID_FEC_CONV_V27P56 | 5/6 | 8.35 | 5.72 | \(K=7\) , \(d_{free}=4\) |
| LIQUID_FEC_CONV_V27P67 | 6/7 | 8.21 | 5.91 | \(K=7\) , \(d_{free}=3\) |
| LIQUID_FEC_CONV_V27P78 | 7/8 | 8.38 | 5.97 | \(K=7\) , \(d_{free}=3\) |
| LIQUID_FEC_CONV_V29P23 | 2/3 | 6.38 | 4.36 | \(K=9\) , \(d_{free}=7\) |
| LIQUID_FEC_CONV_V29P34 | 3/4 | 6.72 | 4.78 | \(K=9\) , \(d_{free}=6\) |
| LIQUID_FEC_CONV_V29P45 | 4/5 | 7.60 | 4.95 | \(K=9\) , \(d_{free}=5\) |
| LIQUID_FEC_CONV_V29P56 | 5/6 | 7.69 | 5.72 | \(K=9\) , \(d_{free}=5\) |
| LIQUID_FEC_CONV_V29P67 | 6/7 | 8.93 | 6.92 | \(K=9\) , \(d_{free}=4\) |
| LIQUID_FEC_CONV_V29P78 | 7/8 | 7.87 | 6.03 | \(K=9\) , \(d_{free}=4\) |
| Reed-Solomon Codes | ||||
| LIQUID_FEC_RS_M8 | 223/255 | 6.04 | - | RS block code, \(m=8\) |
[ref:tab-fec-codecs] lists the available codecs and gives a brief description for each. All convolutional and Reed-Solomon codes are available only if libfec is installed.
[ref:fig-fec-block_ber] ,[ref:fig-fec-conv_ber] , and[ref:fig-fec-convpunc_ber] plot the bit error-rate performance of the forward error-correction schemes available in liquid for a BPSK signal in an AWGN channel. Each figure depicts the BER versus \(E_b/N_0\) (\(E_s/N_0\) compensated for coding rate). The error rates were computed by generating packets of 1024 bits, encoding using the appropriate FEC scheme, modulating the resulting bits with BPSK (see [ref:section-modem-digital-PSK] ), adding noise, demodulating, and decoding. Each point was simulated with a minimum of 4,000,000 trials and a minimum of 1,000 bit errors. The raw data can be found in the doc/data/fec-ber/ subdirectory.
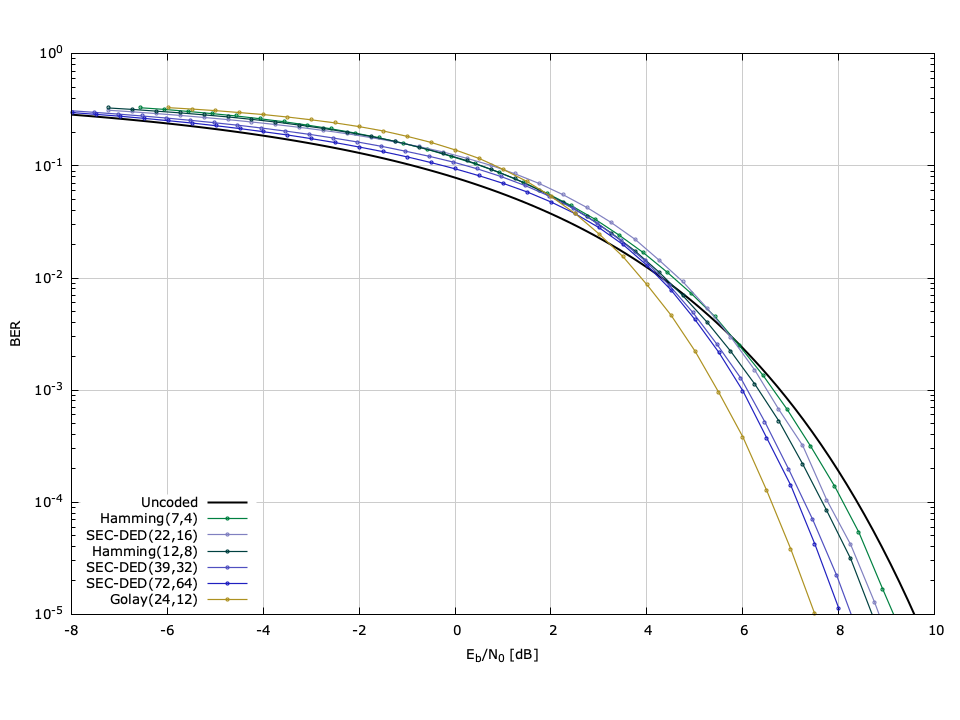
Figure [fig-fec-block_ber]. Forward error-correction codec bit error rates (simulated) for built-in liquid block codecs using BPSK modulation and hard-decision decoding.
[ref:fig-fec-block_ber] depicts the performance of the available built-in liquid FEC codecs, including the Hamming, SEC-DED, and Golay codes. Notice that in terms of \(E_b/N_0\) none of these schemes performs extremely well, perhaps with the exception of the Golay(24,12) code which achieves a BER of \(10^{-5}\) with an \(E_b/N_0\) value of 7.46 dB.
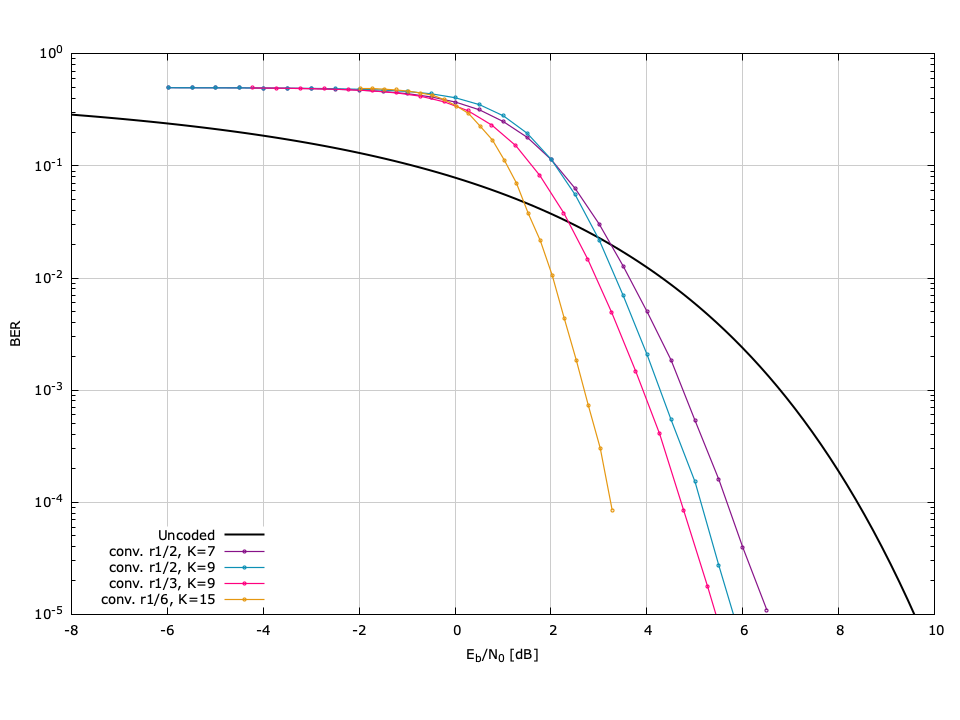
Figure [fig-fec-conv_ber]. Forward error-correction codec bit error rates (simulated) for convolutional codes using BPSK modulation and hard-decision decoding.
[ref:fig-fec-conv_ber] depicts the performance of the convolutional codecs available in liquid when the libfec library is installed. These include LIQUID_FEC_CONV_V27 , LIQUID_FEC_CONV_V29 , LIQUID_FEC_CONV_V39 , and LIQUID_FEC_CONV_V615 . Notice that these codecs provide significant error-correction capabilities over the Hamming codes; this is a result of the fact that convolutional encoding effectively spreads the redundancy over a broader range of the original message, correlating the output samples more than the short-length Hamming codes.
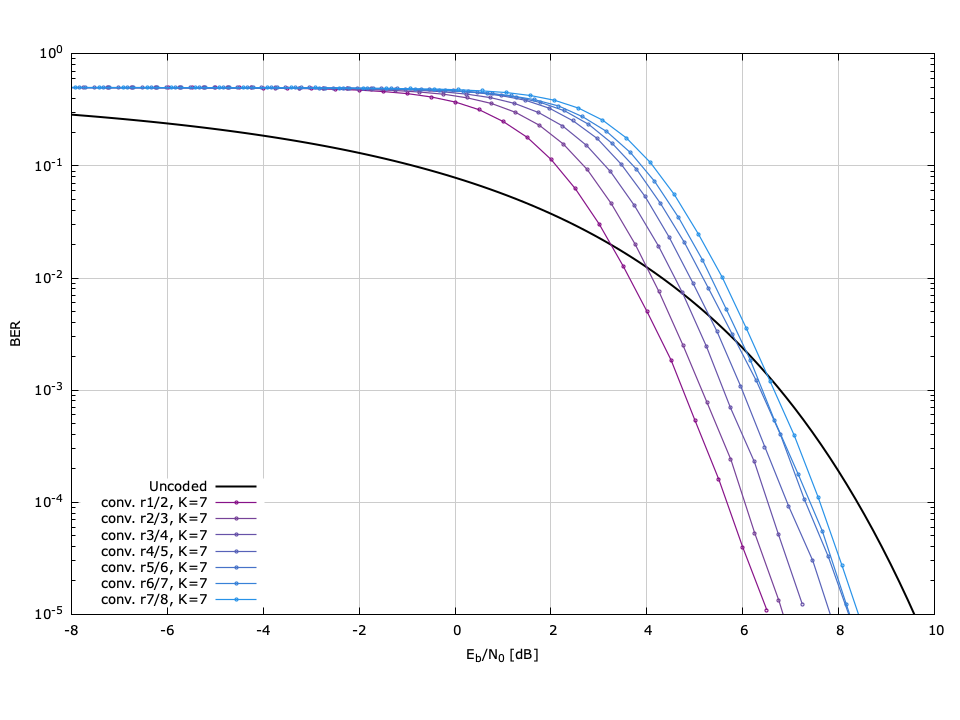
Figure [fig-fec-convpunc_ber]. Forward error-correction codec bit error rates (simulated) for punctured convolutional codes using BPSK modulation and hard-decision decoding.
[ref:fig-fec-convpunc_ber] depicts the performance of the punctured convolutional codecs (\(K=7\) ) available in liquid , also available when the libfec library is installed. These include LIQUID_FEC_CONV_V27P23 , LIQUID_FEC_CONV_V27P34 , LIQUID_FEC_CONV_V27P45 , LIQUID_FEC_CONV_V27P56 , LIQUID_FEC_CONV_V27P67 , and LIQUID_FEC_CONV_V27P78 . Also included is the unpunctured LIQUID_FEC_CONV_V27 codec, plotted as a reference point. liquid also includes punctured convolutional codes for the \(K=9\) encoder; however because the performance is similar to the \(K=7\) codec its performance is omitted for the sake of brevity.