Continuously Variable Slope Delta (CVSD) audio encoder
Keywords: continuous continuously variable slope delta CVSD audio encode audio decode
The audio module in liquid provides several objects and functions for compressing, digitizing, and manipulating audio signals. This is particularly useful for encoding audio data for wireless communications.
Continuously variable slope delta (CVSD) source encoding is used for data compression of audio signals. CVSD is a lossy compression whose quality is directly related to the sampling frequency and is generally most practical for speech applications. It is a form of delta modulation where \(\Delta\) (the step size) is changed continuously to minimize slope-overload distortion {cite:Proakis:2001(p.131)}. The output bit stream has a rate equal to that of the sampling frequency. It is considered to be a moderate compromise between quality and complexity.
Theory∞
The algorithm attempts to dynamically adjust the value of \(\Delta\) to track to the input signal. As with regular delta modulation algorithms, if the decoded reference signal exceeds the input (the error signal is negative), a binary 0 is sent and \(\Delta\) is subtracted from the reference, otherwise a binary 1 is sent and \(\Delta\) is added. However CVSD observes the previous \(N\) transmitted bits are stored in a buffer \(\hat{\vec{b}}\) ;\(\Delta\) is increased by \(\zeta\) if they are equal and decreased otherwise. This improves the dynamic range of the encoder over fixed-delta modulation encoders. A summary of the encoding procedure can be found in[ref:alg-audio-cvsd_encoder] .
.. algorithm [alg-audio-cvsd-encoder]
caption:CVSD encoder algorithm
\algsetup{linenosize=\footnotesize}
\algsetup{linenodelimiter=:}
\algsetup{indent=2em}
\begin{algorithmic}[1]
\STATE $\vec{x} \leftarrow \{x_0,x_1,x_2,\ldots\}$ \COMMENT{input audio samples}
\STATE $v_0 \leftarrow 0$ \COMMENT{initial output reference}
\STATE $\Delta_0 \leftarrow \Delta_{min}$ \COMMENT{initialize step size}
\STATE $\hat{\vec{b}}_0 \leftarrow \{0,0,\ldots,0\}$\COMMENT{initialize $N$-bit buffer}
\FOR{$k=0,\,1,\,2,\,\ldots$}
\STATE $b_k \leftarrow \begin{cases} 0 & v_k \gt x_k \\ 1 & \text{else}\end{cases}$
\COMMENT{compute output bit}
\STATE $\hat{\vec{b}}_k \leftarrow \{\hat{b}_1,\hat{b}_2,\ldots,\hat{b}_{N-1},b_k\}$
\COMMENT{append output bit to end of buffer}
\STATE $m \leftarrow \sum_{i=0}^{N-1}{\hat{\vec{b}}_i}$
\COMMENT{compute sum of last $N$ bits}
\STATE $\Delta_k \leftarrow \begin{cases}\Delta_{k-1}\zeta & m = 0, m=N \\ \Delta_{k-1}/\zeta & \text{else}\end{cases}$
\COMMENT{adjust step size}
\STATE $v_{k+1} \leftarrow v_k + (-1)^{1-b_k} \Delta_k$
\COMMENT{adjust reference value}
\ENDFOR
\end{algorithmic}
The decoder reverses this process; by retaining the past \(N\) bit inputs in a buffer \(\hat{\vec{b}}\) , the value of \(\Delta\) can be adjusted appropriately. A summary of the decoding procedure can be found in[ref:alg-audio-cvsd-decoder] .
.. algorithm [alg-audio-cvsd-decoder]
caption:CVSD decoder algorithm
\algsetup{linenosize=\footnotesize}
\algsetup{linenodelimiter=:}
\algsetup{indent=2em}
\begin{algorithmic}[1]
\STATE $\vec{b} \leftarrow \{b_0,b_1,b_2,\ldots\}$ \COMMENT{input bit samples}
\STATE $v_0 \leftarrow 0$ \COMMENT{initial output reference}
\STATE $\Delta_0 \leftarrow \Delta_{min}$ \COMMENT{initialize step size}
\STATE $\hat{\vec{b}}_0 \leftarrow \{0,0,\ldots,0\}$\COMMENT{initialize $N$-bit buffer}
\FOR{$k=0,\,1,\,2,\,\ldots$}
\STATE $\hat{\vec{b}}_k \leftarrow \{\hat{b}_1,\hat{b}_2,\ldots,\hat{b}_{N-1},b_k\}$
\COMMENT{append output bit to end of buffer}
\STATE $m \leftarrow \sum_{i=0}^{N-1}{\hat{\vec{b}}_i}$
\COMMENT{compute sum of last $N$ bits}
\STATE $\Delta_k \leftarrow \begin{cases}\Delta_{k-1}\zeta & m = 0, m=N \\ \Delta_{k-1}/\zeta & \text{else}\end{cases}$
\COMMENT{adjust step size}
\STATE $v_{k+1} \leftarrow v_k + (-1)^{1-b_k} \Delta_k$
\COMMENT{adjust reference value}
\STATE $y_k \leftarrow v_k$
\COMMENT{set output value}
\ENDFOR
\end{algorithmic}
Pre-/Post-Filtering∞
To preserve the signal's integrity the encoder applies a pre-filter to emphasize the high-frequency information of the signal before the encoding process. The pre-filter is a simple 2-tap FIR filter defined as
$$ H_{pre}(z) = 1 - \alpha z^{-1} $$where \(\alpha\) controls the amount of emphasis applied. Typical values fore pre-emphasis are \(0.92 \lt \alpha \lt 0.98\) ; setting \(\alpha=0\) completely disables this emphasis. This process is reversed on the decoder by applying the inverse of\(H_{pre}(z)\) as a low-pass de-emphasis filter:
$$ H_{pre}^{-1}(z) = \frac{ 1 }{ 1 - \alpha z^{-1} } $$Additionally, the decoder adds a DC-blocking filter to reject any residual offset caused by the decoding process. By itself the DC-blocking filter has a transfer function
$$ H_{0}(z) = \frac{ 1 - z^{-1} }{ 1 - \beta z^{-1} } $$where \(\beta\) controls the cut-off frequency of the filter and is typically set very close to 1. The default value for \(\beta\) in liquid is 0.99. The full post-emphasis filter is therefore
$$ H_{post}(z) = H_{pre}^{-1}(z) H_0(z) = \frac{ 1 - z^{-1} }{ 1 - (\alpha + \beta) z^{-1} + \alpha\beta z^{-2} } $$Interface∞
The cvsd object in liquid allows the user to select both \(\zeta\) as well as \(N\) , the number of repeated bits observed before \(\Delta\) is updated. The combination of these values with the sampling rate yields a speech compression algorithm with moderate quality. Listed below is the full interface to the cvsd object:
- cvsd_create(N,zeta,alpha) creates an agc object with parameters \(N\) , \(\zeta\) , and\(\alpha\) .
- cvsd_destroy(q) destroys a cvsd object, freeing all internally-allocated memory and objects.
- cvsd_print(q) prints the cvsd object's internal parameters to the standard output.
- cvsd_encode(q,sample) encodes a single audio sample, returning the encoded bit.
- cvsd_decode(q,bit) decodes and returns a single audio sample from an input bit.
- cvsd_encode8(q,samples,byte) encodes a block of 8 samples returning the result in a single byte.
- cvsd_decode8(q,byte,samples) decodes a block of 8 samples from an encoded byte.
Example∞
Here is a basic example of the cvsd object in liquid :
#include <liquid/liquid.h>
int main() {
// options
unsigned int nbits=3; // number of adjacent bits to observe
float zeta=1.5f; // slope adjustment multiplier
float alpha = 0.95; // pre-/post-filter coefficient
// create cvsd encoder/decoder
cvsd q = cvsd_create(nbits, zeta, alpha);
float x; // input sample
unsigned char b; // encoded bit
float y; // output sample
// ...
// repeat as necessary
{
b = cvsd_encode(q, x); // encode sample
y = cvsd_decode(q, b); // decode sample
}
cvsd_destroy(q); // destroy cvsd object
}
A demonstration of the algorithm can be seen in[ref:fig-audio-cvsd] where the encoder attempts to track to an input sinusoid. Notice that the encoder sometimes overshoots the reference signal. This distortion results in degradations, particularly in the upper frequency bands.
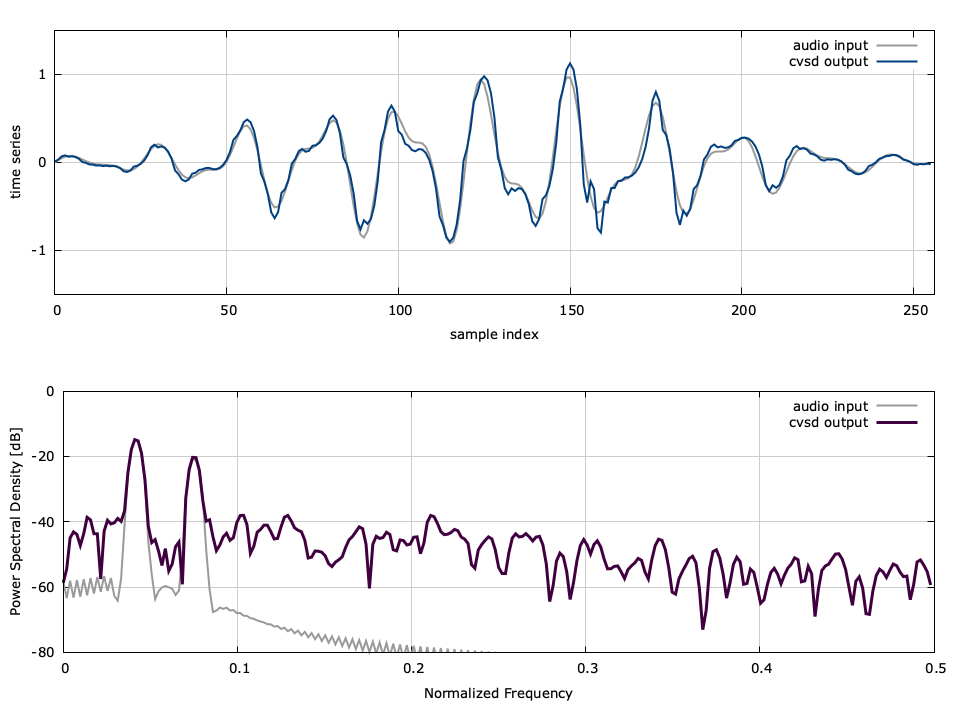
Figure [fig-audio-cvsd]. cvsd example encoding a windowed sum of sine functions with \(\zeta=1.5\) , \(N=2\) , and \(\alpha=0.95\) .
A more detailed example is given in examples/cvsd_example.c under the main liquid project directory.