Complementary Codes

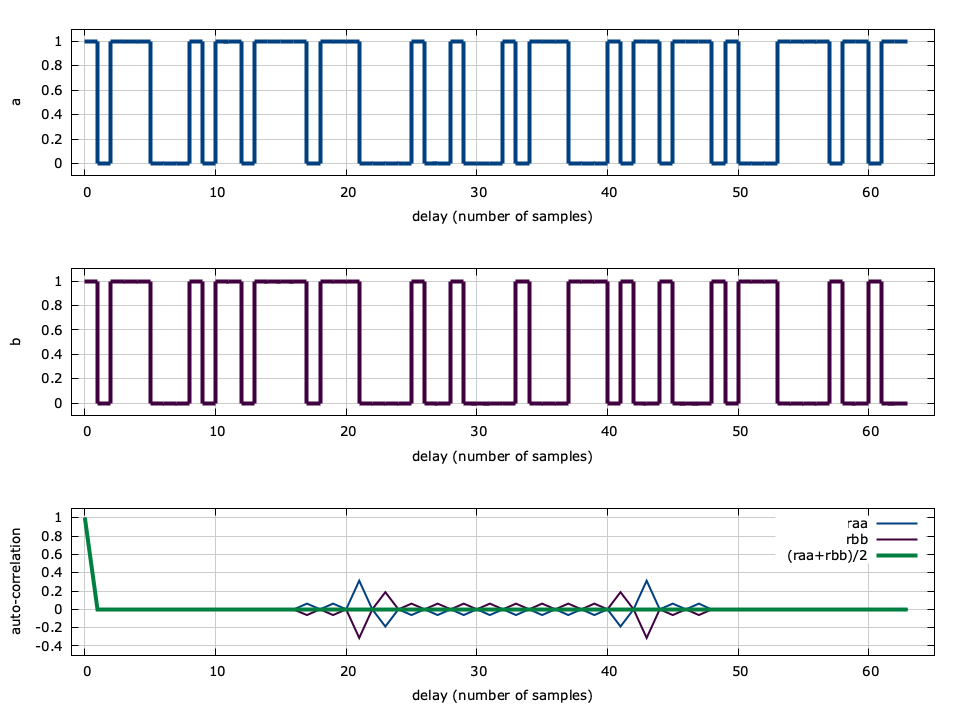
In addition to maximal-length sequences, liquid also implements complementary codes: P/N sequence pairs which have similar properties to m-sequences. A complementary code pair is one in which the sum of individual auto-correlations is identically zero for all delays except for the zero-delay which provides an auto-correlation of unity. The two codes \(\vec{a}\) and \(\vec{b}\) are generated recursively as

$$ \vec{a}_{k+1} = \left[ \vec{a}_k \,\,\, \vec{b}_k \right] $$ $$ \vec{b}_{k+1} = \left[ \vec{a}_k \,\,\, \bar{\vec{b}}_k \right] $$

where \([\cdot,\cdot]\) represents concatenation and\(\bar{(\cdot)}\) denotes a binary inversion.[ref:tab-sequence-ccodes] shows the first several iterations of the sequence. Notice that the sequence length doubles for each iteration, and that (with the exception of \(k=0\) ) the first half of \(\vec{a}_k\) and \(\vec{b}_k\) are identical.[ref:fig-sequence-ccodes] shows that the auto-correlation of the two sequences is non-zero for delays other than zero, but that they indeed do sum to zero.

Table [tab-sequence-ccodes]. Default complementary codes in liquid

Iteration	\(\vec{a}\)	\(\vec{b}\)
1	1	0
2	10	11
4	1011	1000
8	10111000	10110111
16	10111000 10110111	10111000 01001000
32	10111000 10110111 10111000 01001000	10111000 10110111 01000111 10110111
64	10111000 10110111 10111000 01001000 10111000 10110111 01000111 10110111	10111000 10110111 10111000 01001000 01000111 01001000 10111000 01001000