Simplified Phase-locked Loop in C
Keywords: phase-locked loop design PLL
Update (14 Jan 2017) : I modified the loop filter design to be more consistent with common terminology in the literature.
If you read my last tutorial on writing a PLL in C and found it overly complex, this entry should hopefully clear some of that up. I received a lot of feedback on it and realize that I tend to make things unnecessarily complicated. Sorry.
So here is a super simple phase-locked loop in 50 lines of C. I've omitted the lengthy, boring, math (no more Laplace transforms!) and boiled down the PLL to its bare essentials. It's definitely a lot easier to understand, especially if you haven't had 3 semesters of electrical engineering courses to prepare you. I won't even include any equations (ok, maybe one).
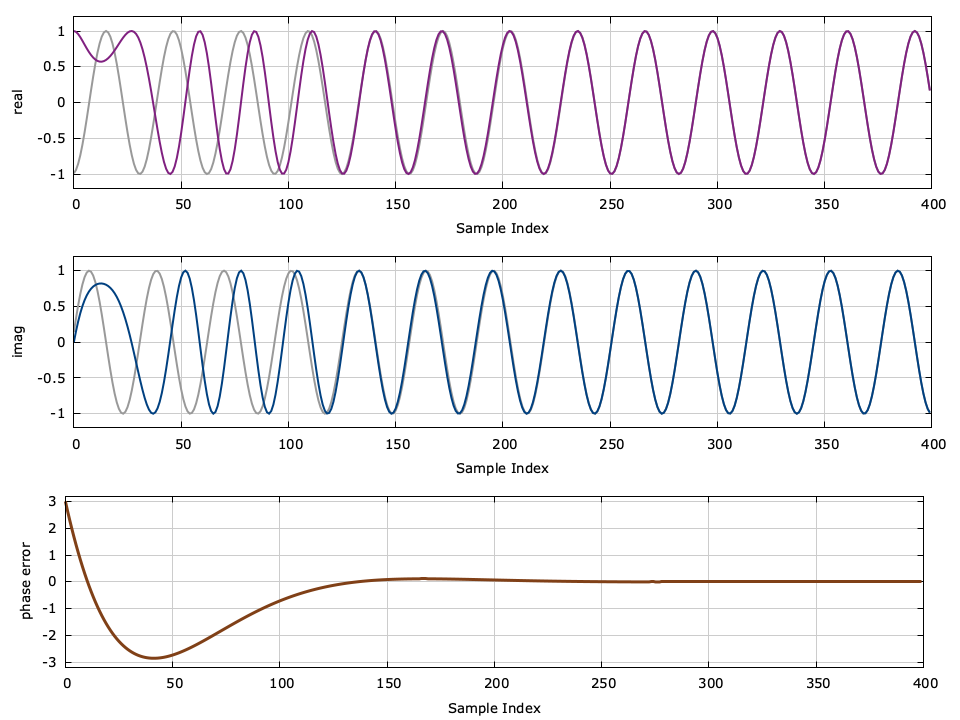
You can download a tarball of this example which includes all the source code here: liquid_pll_simple_example.tar.gz . Running the program should produce an image that looks like this:
Problem statement∞
I have an incoming complex sinusoid with an unknown but constant frequency and phase (and it's possibly noisy, but we won't add noise in our example). I want to track the phase of this input on a sample-by-sample basis. Basically I need to generate a new sinusoid (the output) that has the exact same phase and frequency as the input.
The concept of a PLL is simple:
- Make a measurement of the phase error between the input signal and my output sinusoid.
- Adjust my output signal's frequency and phase proportional to this phase error.
- Repeat.
Sounds simple enough, right? The difficulty is knowing precisely how to execute step 2 to get the output to converge and not blow up (that's where all that math from the previous post came in). There's a simple trick to you can use to get really good performance:
- Define a variable \(\alpha\) as the the proportion of the phase error we will apply to adjust our output phase . Note that \(\alpha\) is proportional to the loop filter bandwidth and so it should be relatively small (e.g. 0.05 or so).
- Define a new variable \(\beta = \alpha^2/2\) . This value will be the proportion of the phase error we will apply to adjust our output frequency .
Source Code Breakdown∞
So here's the program in 50 lines (as promised):
// pll_simple_example.c : simulation of a phase-locked loop in 50 lines
// [update] 14 Jan. 2017: updated loop filter to be consistent with literature
#include <stdio.h>
#include <stdlib.h>
#include <complex.h>
#include <math.h>
int main() {
// parameters and simulation options
float phase_in = 3.0f; // carrier phase offset
float frequency_in = -0.20; // carrier frequency offset
float alpha = 0.05f; // phase adjustment factor
unsigned int n = 400; // number of samples
// initialize states
float beta = 0.5*alpha*alpha; // frequency adjustment factor
float phase_out = 0.0f; // output signal phase
float frequency_out = 0.0f; // output signal frequency
// print line legend to standard output
printf("# %6s %12s %12s %12s %12s %12s\n",
"index", "real(in)", "imag(in)", "real(out)", "imag(out)", "error");
// run basic simulation
int i;
for (i=0; i<n; i++) {
// compute input and output signals
float complex signal_in = cexpf(_Complex_I * phase_in);
float complex signal_out = cexpf(_Complex_I * phase_out);
// compute phase error estimate
float phase_error = cargf( signal_in * conjf(signal_out) );
// print results to standard output for plotting
printf(" %6u %12.8f %12.8f %12.8f %12.8f %12.8f\n",
i,
crealf(signal_in), cimagf(signal_in),
crealf(signal_out), cimagf(signal_out),
phase_error);
// apply loop filter and correct output phase and frequency
phase_out += alpha * phase_error; // adjust phase
frequency_out += beta * phase_error; // adjust frequency
// increment input and output phase values
phase_in += frequency_in;
phase_out += frequency_out;
}
return 0;
}
Compiling and running the program will produce an output data file should look similar to this:
# index real(in) imag(in) real(out) imag(out) error
0 -0.98999250 0.14112000 1.00000000 0.00000000 3.00000000
1 -0.94222230 0.33498821 0.98820370 0.15314497 2.64625001
2 -0.85688871 0.51550144 0.95734698 0.28894085 2.30687952
3 -0.73739362 0.67546326 0.91373789 0.40630421 1.98159420
4 -0.58850098 0.80849653 0.86285567 0.50545037 1.67009592
5 -0.41614661 0.90929753 0.80925429 0.58745849 1.37208498
6 -0.22720182 0.97384769 0.75657302 0.65390921 1.08725977
...
394 0.92037261 -0.39104259 0.92032784 -0.39114791 0.00011444
395 0.82433999 -0.56609505 0.82427084 -0.56619567 0.00012207
396 0.69544452 -0.71857977 0.69535130 -0.71867001 0.00012973
397 0.53882474 -0.84241790 0.53870904 -0.84249187 0.00013733
398 0.36072436 -0.93267244 0.36058915 -0.93272477 0.00014499
399 0.16824348 -0.98574549 0.16809307 -0.98577112 0.00015259
Ideally when the simulation is finished, the input phase and output phase should be equal (modulo \(2\pi\) ) and so should the input/output frequencies. From the results we can make a few observations:
- The phase error at the first step is exactly 3 radians, the input phase.
- The magnitude of the error drops, on average, with each step.
- The signals are nearly identical by the last iteration.
So why didn't I present this simpler, more elegant PLL design in my previous post ? Chalk it up to being in academia too long.